This is the third part of a series of posts showing how to visually represent the four operations of whole numbers using the CHIP MODEL. The first part shows how to model addition and subtraction. The second part demonstrates multiplication with the chip model.
There are two ways to think of division: partitive and quotitive. While both ways lead to the correct answer, the distinction between the two is incredibly important in developing students who are mathematically flexible.
Partitive is also called fair share or sharing. Quotitive is also called repeated subtraction or measurement.
|
Partitive |
Quotitive |
|
If I sort 12 dots into 3 equal groups, how big is each group? |
If I sort 12 dots into groups of 3, how many groups will there be? |
|
|
|
|
12 ÷ 3 = 4 There are 4 dots in each group. |
12 ÷ 3 = 4 There are 4 groups. |
The distinction between types of division is more than just a semantic difference. Word problems often almost always have a context that more easily lends itself towards partitive thinking or quotitive thinking.
“Three friends equally share 27 gumballs such that each friend gets the same number of gumballs. How many gumballs does each friend get?”
This context is an example of partitive division because the 27 gumballs are being sorted into three equal parts.
“Rosa picked 27 apples from her apple tree. She wants to put those apples in gift bags to give to her friends. If she puts 3 apples in each bag, how many bags will she need?”
This context is an example of quotitive division because the 27 apples are being sorted into groups of three.
Let’s examine the following division problem through both types of division.
We begin with the partitive method of division.
|
Begin by modeling 579 on the place value chart. |
|
|
Partitive division means were are fair sharing amongst a known number of groups, so we create four groups because we are dividing by 4. |
|
|
There are 5 hundreds, so we can put 1 dot in each of the four groups with one dot remaining. That one remaining hundred can be exchanged for 10 tens in the next column over. Remember, 1 big is exchanged for 10 littles. |
|
|
There are now 17 tens, so we can put 4 dots in each group with one dot remaining. That one remaining ten can be exchanged for 10 ones in the next column over.
|
|
|
There are now 19 ones to sort into the four groups. Each group has 4 dots with 3 dots left over. |
|
|
The resulting visual representation shows that in each of the four groups is 1 hundred, 4 tens, and 4 ones with 3 ones remaining Or more simply… 144 r3 |
|
Here is a video demonstrating the partitive approach…
Here we look at the same division problem, however, this time we solve the problem using the quotitive method.
|
Begin by modeling 579 in the place value chart. |
|
|
Quotitive division means were are sorting each place value of 579 into groups of 4 because we are dividing by 4. There are 5 hundreds, which enables us to circle 1 group. The remaining hundred is exchanged for 10 tens in the next column over. |
|
|
There are now 17 tens, which can be sorted into 4 groups. The remaining ten is exchanged for 10 ones in the next column over. |
|
|
There are now 19 ones, which can be sorted into 4 groups. There are 3 ones remaining. |
|
|
The resulting visual representation shows that there is 1 group in the hundreds column, 4 groups in the tens column, 4 groups in the ones column, and 3 ones remaining. Or more simply… 144 r3 |
|
Notice that all the work students would be doing is with the dots. We haven’t actually recorded any of the steps in the standard algorithm. This is by design! We need to give students plenty of experience with the visual models of division to make sense of the math concept BEFORE moving to the more abstract algorithm.
Eventually, students will show the chip model and the algorithm side-by-side, using the chip model on the left and recording each step with numbers on the right side.
|
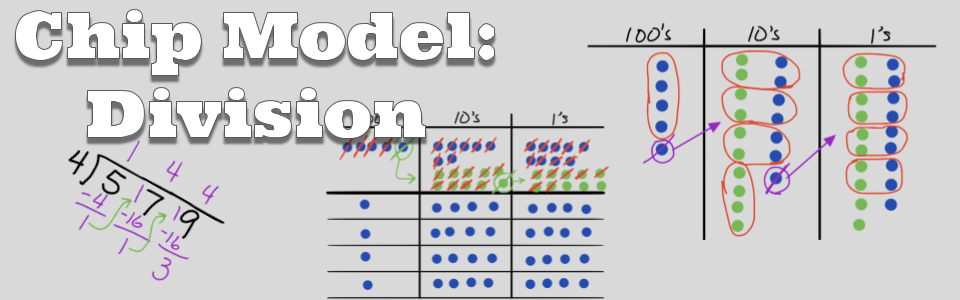
We begin by modeling 579 on the place value chart. Notice the dots are arranged in vertical lines. This is not mathematically different than previous examples and is done only make the connection to the algorithm easier to see. |
|
|
Step 1: Divide the hundreds into 1 group with one dot left over. That dot is exchanged for 10 tens. Notice the algorithm in brings the 1 hundred up to the tens column to create 17 tens. This is in contrast to the more common method of dropping the 7 tens down to create 17 tens. |
|
|
Step 2: Divide the tens into 4 groups with one dot left over. That one dot is exchanged for 10 ones. There are now 19 ones in the ones column. |
|
|
Step 3: The 19 ones are sorted into 4 groups with three dots left over. Take a moment to examine how the visual representation on the left relates to the algorithm on the right. |
|
Here is a video showing how to do the quotitive approach to division.
What would it look like to divide by a two-digit number? Here is the video for that…
To summarize this section on division, there are two things for students to know:
- Division means to create equal groups with partitive thinking or quotitive thinking
- 1 big can be exchanged for 10 littles
.
.
.