Teaching Through Problem-Solving

The report, Adding It Up: Helping Children Learn Mathematics, begins with a strong statement, “All young Americans must learn to think mathematically, and they must think mathematically to learn.” Adding It Up breaks down what it means to think mathematically into several strands of proficiency. These abilities are described as five interwoven and interdependent strands. The report defines them as:

• conceptual understanding – comprehension of mathematical concepts, operations, and relations
• procedural fluency – skill in carrying out procedures flexibly, accurately, efficiently, and appropriately
• strategic competence – ability to formulate, represent, and solve mathematical problems
• adaptive reasoning – capacity for logical thought, reflection, explanation, and justification
• productive disposition – habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy

However, the common pedagogical strategy of teacher lecture followed by student procedural practice cannot nurture all five strands of proficiency.

In this post I want to share with you Teaching Through Problem-Solving (TTP) an alternative to the teacher-dominated, lecture-based instruction that is commonplace in math classrooms.

First I’ll clarify what I mean by “teacher-dominated, lecture-based instruction”. This sort of instruction is often called “I do, We do, You do”. The teacher first models the process (I Do), then invites the students in performing the procedure together as a whole class (We Do), and finally lets students perform the procedure independently (You Do).  This sort of teaching invites students to spend most of their time doing exercises – completing problems for which a solution method has already been taught.

It also does not create space for students to develop strategic competence and adaptive reasoning. After all, the entire purpose of “I do, We do, You do” is to avoid the productive struggle students necessarily must experience in order for them to develop those proficiencies.

So, if the most common form of math instruction (I do, We do, You do) is not going to produce the results we want, what are we to do? What should teaching look like?

Research in the fields of education and psychology show that students learn best through active engagement and investigation in which students solve problems before a “official” solution method or procedure is taught by the teacher. In a nutshell, this is Teaching Through Problem-Solving.

What is Teaching Through Problem-Solving?

Teaching Through Problem Solving (TTP) is an advanced pedagogical approach that enables teachers to create an environment for students to become proficient in those five interdependent proficiency strands. In TTP, teachers introduce new mathematical concepts by giving students new problems to try to solve on their own. The teacher doesn’t act as a lecturer, but instead observe students as they work independently and facilitates a whole class discussion of their solution approaches. Asking students to wrestle directly with new concepts in thai way imparts the mathematical thinking skills they need to become active and engaged learners.

In a lesson that follows the TTP instructional principles,

• students learn new mathematics by solving problems prior to the teacher instruction
• students struggle with a novel problem, present and discuss solution strategies, and together build the next concept or procedure in the mathematics curriculum
• real contexts, problems, situations, and models are used to provide students with an informal access (low floor) to the concept they are learning
• the contexts and models allow students to build meaning for the concepts so that they can move to abstract concepts (high ceiling).

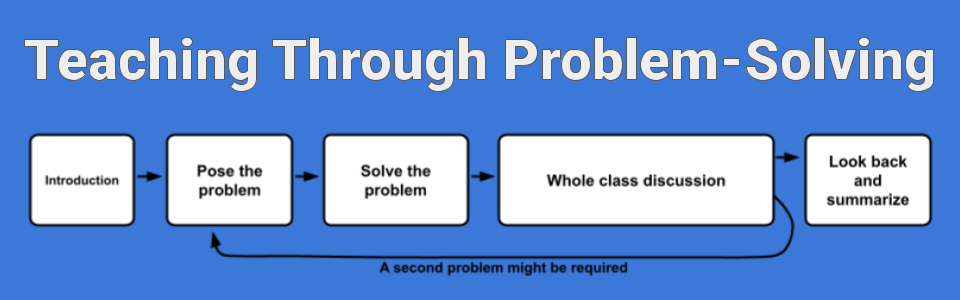
A typical 45-60 minute TTP lesson format has five components:

Teachers guide the lesson through each of the five components…

A recent classroom example of the 5 components of TTP

Here I will share a recent example of me using the TTP lesson design in an actual classroom. As I describe the experience, I’ll also indicate each of the five lesson components.

The other day I was in a 2nd grade classroom. The teacher was struggling to help the students understand that sometimes it is easier to solve a subtraction problem by thinking about it as an addition problem with a missing addend. On the front whiteboard she had written 43 – 27 and its related addition problem.

The teacher wanted students to model their thinking with a number line.

Introduction

At the invitation of the teacher, I changed gears and asked students to take out their personal whiteboards and draw an empty number line on it. I modeled the number line on the whiteboard in the front of the room for students to see and placed 27 and 43 on the numberline. Students did the same on their own whiteboards. This was my attempt at reminding students that they have spent the previous day or two learning how to represent numbers on a number line.

Then I drew a frog on top of each number.

Pose the problem

Almost immediately I heard at least one student mumble “How far apart are they?” as I was posting the following prompt:

I wondered aloud how many hops Frog A (pointing at 27) would need to take to join Frog B (pointing at 43). I told students they could use whatever counting strategy they wanted.

Solve the problem

I then gave students silent time to work on this problem individually. After about 90 seconds students were allowed to compare their strategies and answers with an elbow partner.

As students were working individually and in pairs, I walked around the room to monitor students and notice the solution approaches being used. I selected two students to share their thinking and planned the order in which they would share.

Whole class discussion

Even though not every student had an answer – and many of the answers students did have were incorrect – I asked students to put down their markers because two students were going to share their solution strategies.

I called Student A to the front with her personal whiteboard to show the class. Then she replicated her work on the number line I had quickly drawn on the big whiteboard in the front of the room.

I then invited Student B to share his solution strategy on a second number line I had quickly drawn on the board.

At this point, the two students shared their thinking on the board, but we did not yet do much (if any) checking for understanding with the rest of the students. I just wanted to get the two strategies side-by-side.

The real mathematical discussion began after students shared their solution approaches. I wanted to engage the students in a discussion that would lead the students to help each other and to develop a deep understanding of the math concept at hand.

I wanted to avoid me explaining the student work to the class and instead have the students do the explaining of the approaches. Ideally, I wanted to see students building upon each other’s ideas and asking questions about each other’s work.

There are four main types of whole-class discussion in a TTP lesson…

1. Address several different approaches to the problem in sequence, starting with the most basic and leading up to the most sophisticated in order to examine the progression of thought.
2. Compare the different approaches side by side to help students find the relationships between them.
3. Contrast two approaches to highlight typical misconceptions and misunderstandings (debate).
4. Compare multiple different solutions using an open-ended problem to identify general rules or characteristics.

I decided I would try to facilitate a Type 2 conversation where the students would compare and contrast the two approaches on the board. We started by noticing things the two strategies had in common. Then we shifted to noticing how the two methods were different.

Look back and summarize

As the conversation drew to a close, I returned to the original expressions the teacher had written on the board: 43 – 27 = [     ] and 27 + [     ] = 43

“What number goes in the box?”, I asked. 16 was the universal response. I wanted students to summarize the main point of this lesson, but they did not yet have the words to express themselves. Truthfully, I wasn’t sure myself what the main point was.

Upon reflection, I wanted students to say something along the lines of “Sometimes when we have to find the answer to a subtraction problem, it is easier to think of it as an addition problem on a number line.”

Students were ready to work on a second problem, so they erased their personal whiteboards and drew a new number line on it.

I posted a second problem for students to solve and repeated the prompt, “How many hops will it take for Frog A to reach Frog B?”

Students again initially worked independently before joining their elbow partner a minute or two later.

Nearly every student used one of the two methods shared during our first problem and arrived at the correct solution of 17.

By now we had spent just about 45 minutes going very, very deep on just two examples. And yet, I felt comfortable that students learned the lesson’s objective and had plenty of practice as well.

To wrap this up:

We want students to have conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and a productive disposition. But our old fashioned approach to  instruction is not going to get us there. Teaching Through Problem-Solving is an advanced pedagogical approach that will. Now it is just up to us adults to be willing to learn this new strategy.

Feel free to contact the MCOE Math Team if you are interested in learning more about TTP.

.

.

.