Take a moment to solve this problem using any method you wish…
A farm has a total of 480 llamas and alpacas.
\(\frac{4}{5}\) of the number of llamas at the farm are equal to \(\frac{4}{7}\) of the number of alpacas.
How many more alpacas than llamas are there?
I’ll wait.
.
.
.
.
.
Can I move on?
It is likely you tried some sort of algebra. If so, it might have looked a little like this…
Gross.
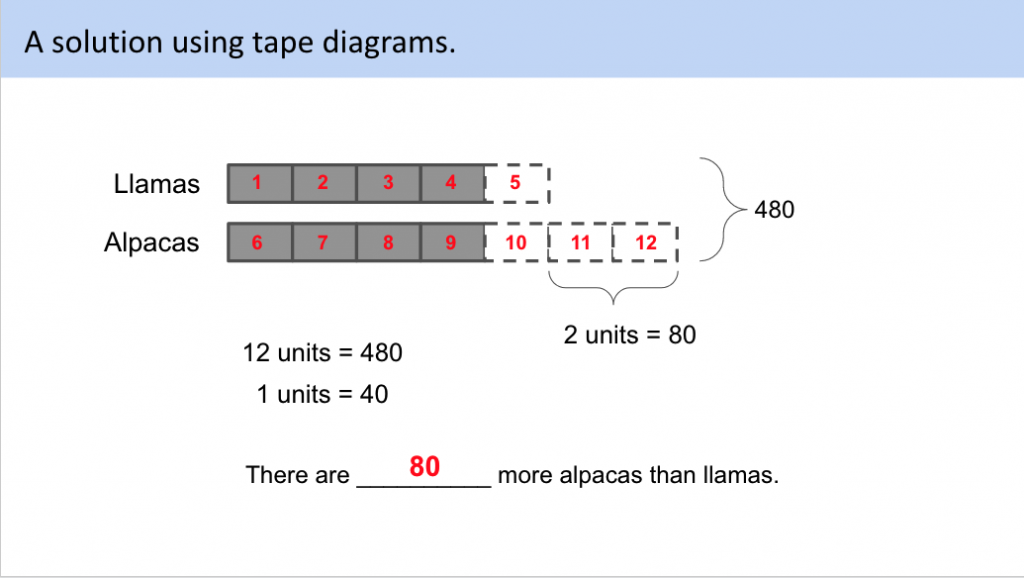
Using tape diagrams, it would look like this…
Take a moment to look at the tape diagram above.
What do you notice? What do you wonder?
.
.
.
Using tape diagrams, this problem requires no mathematics beyond 4th grade division and 4th grade fractions. The SAME problem can be solved using fancy algebra or simple arithmetic.
In a nutshell, tape diagrams increase access to rigorous mathematics for ALL students.
Look forward to an upcoming announcement for a fantastic workshop on tape diagrams.
.
.
.