2023-2024 Archive problems
2022-2023 Archive problems
2021-2022 Archive problems
2020-2021 Archive problems
Word problems. Ugh!
How often have you heard that in your classroom. Heck…I certainly heard it uttered numerous times in my own classroom. In fact, there are many times in which I was the one doing the complaining.
Oh, how I wish I was taught how to use tape diagrams to solve word problems. Unfortunately, it was not until deep into my career as a math teacher that I learned about this awesome tool for solving word problems.
A tape diagram is a model that pictorially represents a word problem. Once the word problem is accurately modeled, the student has an easier time seeing which operations to use in solving the problem. The tape diagram does not do the calculations for the student, but it does make it easier for the student to see which calculations might be needed.
Tape diagrams are especially useful for modeling addition, subtraction, multiplication, division, fractions, and ratios/proportions.
 8-step model method
8-step model method
Long ago I was introduced to the 8-step modeling method. I don’t know for sure, but I think the eight steps were originally from this book by Bob Hogan and Char Forsten. As the name suggests, it is eight wonderful steps that guide the student to drawing a pictorial model of the word problem. As students read and re-read the problem, it becomes more of a story and less of a problem.
1. Read the entire problem.
2. Turn the question into a sentence with a space for the answer.
3. Determine who and what is involved in the problem.
4. Draw unit bars of equal length.
5. Re-read each sentence one at a time and revise the bar(s).
6. Put the question mark in place.
7. Work computations to the side.
8. Write down your answer to the problem.
Addition
Let’s dig into each of these eight steps using the following 2nd grade addition problem:
Brienne has 23 fewer pennies than Alonzo. Alonzo has 45 pennies. How many pennies do Alonzo and Brienne have altogether?
Step 1: Read the entire problem.
Students will find themselves reading the story numerous times. Each time will have a different purpose in the model drawing process.
Step 2: Turn the question into a sentence with a space for the answer.
![]()
Step 3: Determine who and what is involved in the problem.

Step 4: Draw unit bars of equal length.

Step 5: Re-read each sentence one at a time and revise the bar(s).
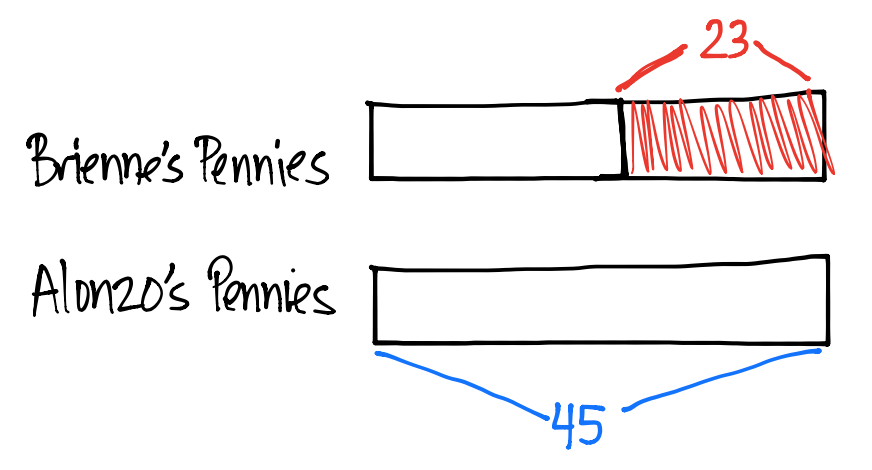
NOTE: There are often more than one way to revise the bars to match the story. For example, rather than shortening Brienne’s bar, we could have lengthened Alonzo’s.
Step 6: Put the question mark in drawing. Optional: Use letters to represent the unknown(s).
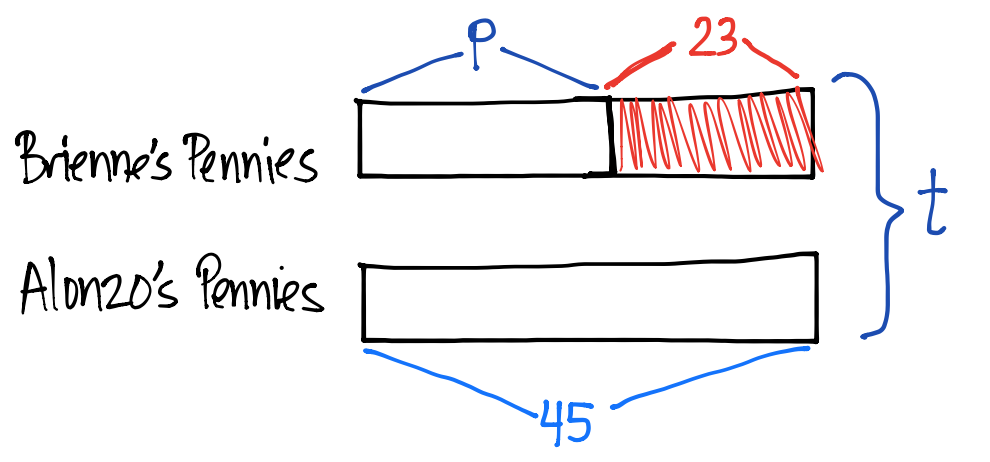
Step 7: Work computations to the side.
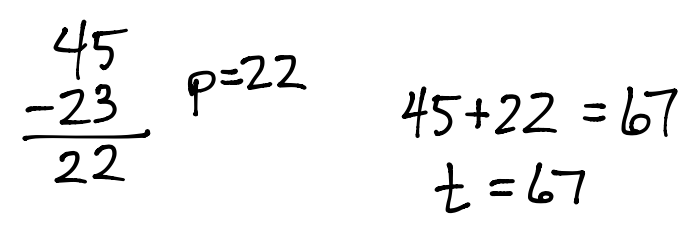
Step 8: Write down your answer to the problem.
![]()
As students continue using the eight steps to represent word problems, students will also begin to notice that word problems using addition and subtraction begin to have a common look about them.
Here is a wonderful online tool for practicing drawing models for addition and subtraction problems.
https://www.mathplayground.com/tb_addition/index.html
To help students remember the eight steps, consider prominently displaying this poster showing each of the steps.

http://bit.ly/wordproblem8steps
Students might also benefit from using a graphic organizer that shows each of the steps and provides workspace too.

Just as addition and subtraction tape diagrams have common characteristics, multiplication and division tape diagrams will also look similar to one another.
Let’s take a look at a multiplication problem. In this case all eight steps are completed at once.
At lunch recess, Karen passed out 3 times as many cookies as Vido did. If Vido passed out 35 cookies, how many cookies did they pass out altogether?
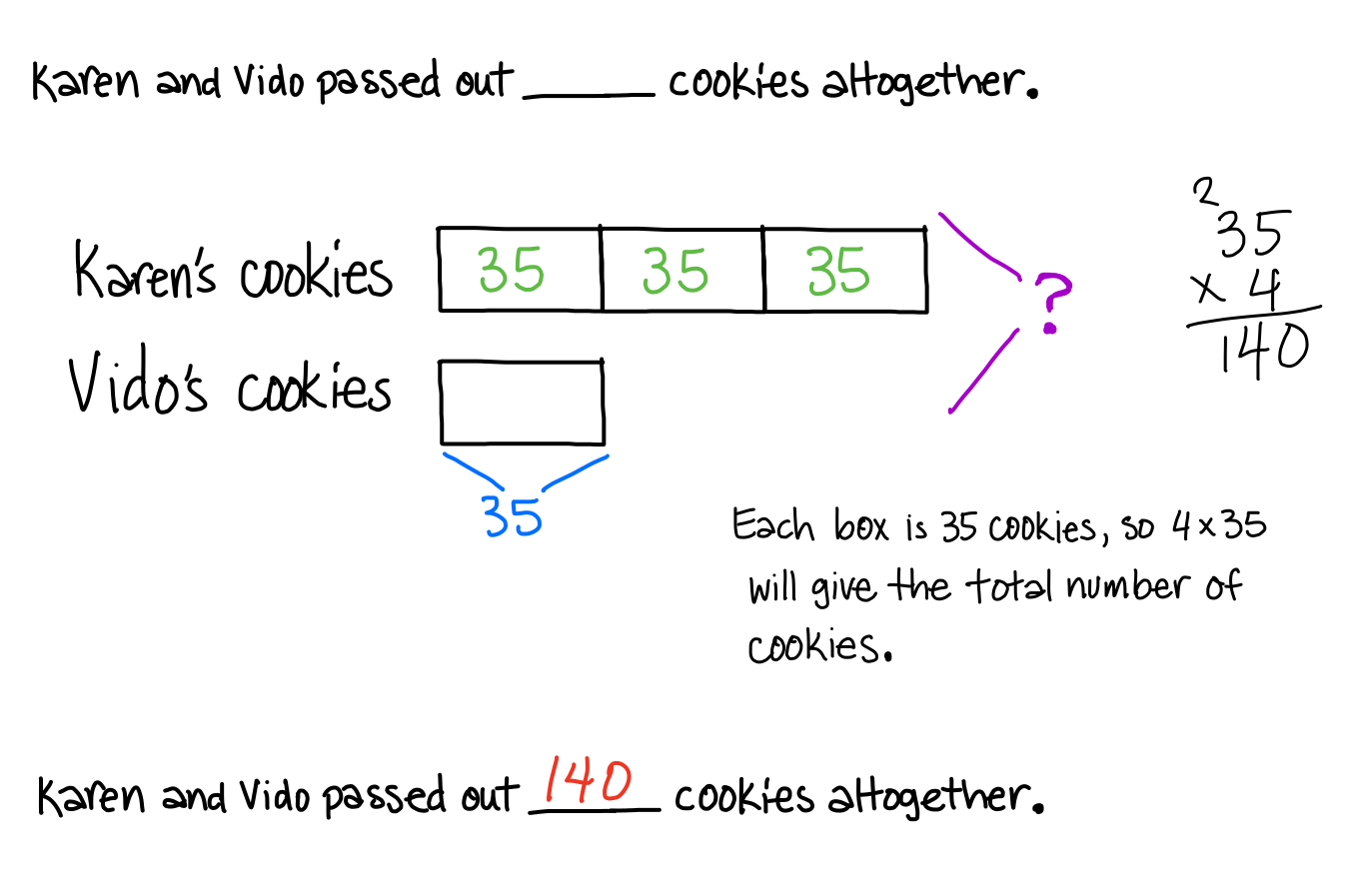
Take a moment to practice multiplication and division problems here.
https://www.mathplayground.com/tb_multiplication/index.html
Fractions
Ella has a collection of toys. After giving ⅗ of her collection to her younger brother, she had 6 toys left. How many toys did Ella give to her younger brother?
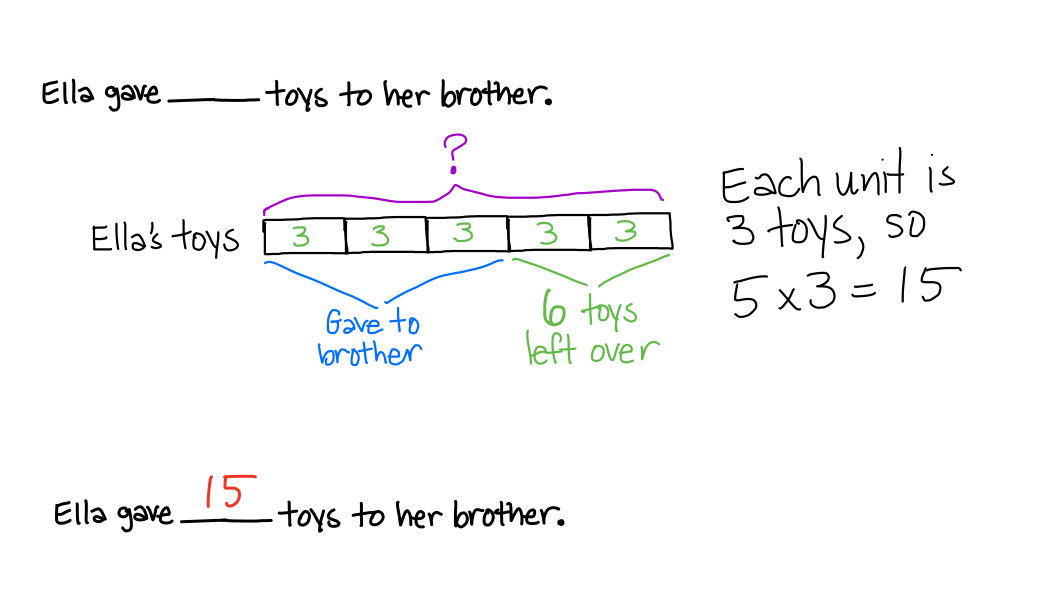
Try some fraction modeling here.
https://www.mathplayground.com/tb_fractions/index.html
Ratios and proportions
Lastly, let’s look at a problem involving ratios.
In the orchestra at Willard Middle School, the ratio of girls to boys is 5 to 3. There are 28 more girls than boys in the orchestra. How many students are in the orchestra altogether?
The initial answer statement and model might look like this…
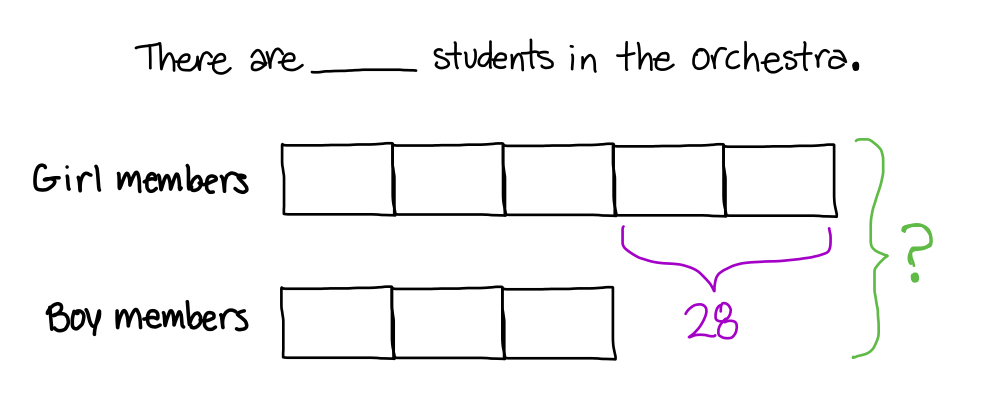
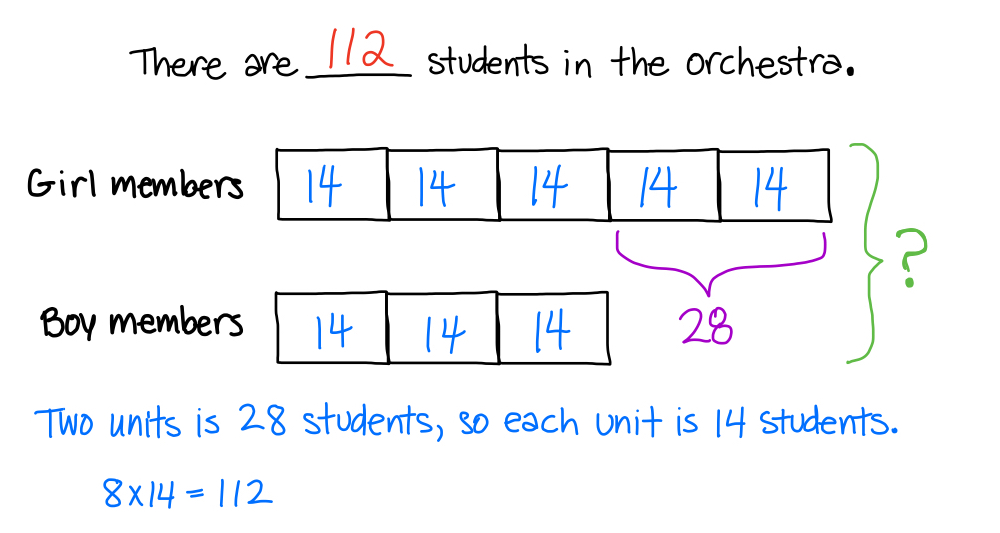
Once the problem has been modeled, we see that two units represents 28 students. The model with some worked filled in might look like this…
Practice modeling ratio problems here.
https://www.mathplayground.com/tb_ratios/index.html
Practice time
So, now you have seen an example from each of the variety of problems for which tape diagrams are particularly useful. Now it is time to practice!
Here are example problems taken from Eureka Math. Give them a try!
Nikil baked 5 pies for the contest. Peter baked 3 more pies than Nikil. How many pies did Peter bake for the contest? (G1 M6 L2)
Eighty-two students are in the math club. 35 students are in the science club. How many more students are in the math club than science club? (G2 M4 L16)
Mr. Nguyen fills two inflatable pools. The kiddie pool holds 185 liters of water. The larger pool holds 600 liters of water. How much more water does the larger pool hold than the kiddie pool? (G3 M2 L19)
Jayden has 347 marbles. Elvis has 4 times as many as Jayden. Presley has 799 fewer than Elvis. How many marbles does Presley have? (G4 M3 L12)
Mrs. Onusko made 60 cookies for a bake sale. She sold ⅔ of them and gave ¾ of the remaining cookies to the students working at the sale. How many cookies did she have left? (G5 M4 L16)
Mason and Laney ran laps to train for the long-distance running team. The ratio of the number of laps Mason ran to the number of laps Laney ran was 2 to 3. Mason ran 6 miles. How much further did Laney run than Mason? (G6 M1 L3)
Jillian exercises 5 times a week. She runs 3 miles each morning and bikes in the evening. If she exercises a total of 30 miles for the week, how many miles does she bike each evening? (G7 M2 L17)
Monica and Naomi had the same amount of money. After Monica spent $25 and Naomi spent $36, Monica had 2 times as much money as Naomi. How much money did each have at first? (G8…not from Eureka Math)
In a school choir, one-half of the members were girls. At the end of the year, 3 boys left the choir, and the ratio of boys to girls became 3:4. How many boys remained in the choir? (Algebra, Module 1, Lesson 25)
.
.
.
