I recently was hanging out with some 6th grade teachers and, as often happens with teachers, we began talking shop.
“Fractions…ugh”, said one teacher. “I’m getting into dividing fractions. I don’t know how to explain it to my kids any better than KEEP-CHANGE-FLIP”, she confessed.
“I don’t teach that algorithm, because it never makes sense to my students”, chimed a second teacher. “Instead”, she continued, “I use the common denominator method.”

A collective “Huh?” spread through the room. She went to the whiteboard and wrote this…
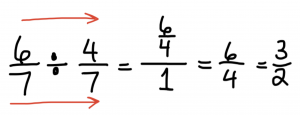
After doing a few examples, the teachers were pretty excited about the prospects of dropping the KEEP-CHANGE-FLIP mystery in exchange for this new method. That’s when I played the role of buzz-kill and asked “Why does this work?”
![]()
Uh…deer in the headlights.
Here’s the deal
In our search for alternative algorithms, we cannot merely exchange one meaningless algorithm with an alternative meaningless algorithm.
In our search for alternative algorithms, we cannot merely exchange one meaningless algorithm with an alternative meaningless algorithm. The purpose of alternative algorithms is to find ways to unveil the MEANING of mathematics. Often, our traditional algorithms have become the preferred algorithm because they are so efficient. But it is exactly that efficiency that obfuscates the underlying conceptual understanding of the math. If we are to use an alternative algorithm (heck…if we use ANY algorithm), we must allow students to see WHY that algorithm makes mathematical sense.
Inspired by the conversation of these awesome 6th grade teachers, I made this video explaining how common denominators can be used to divide fractions.
.
.
.
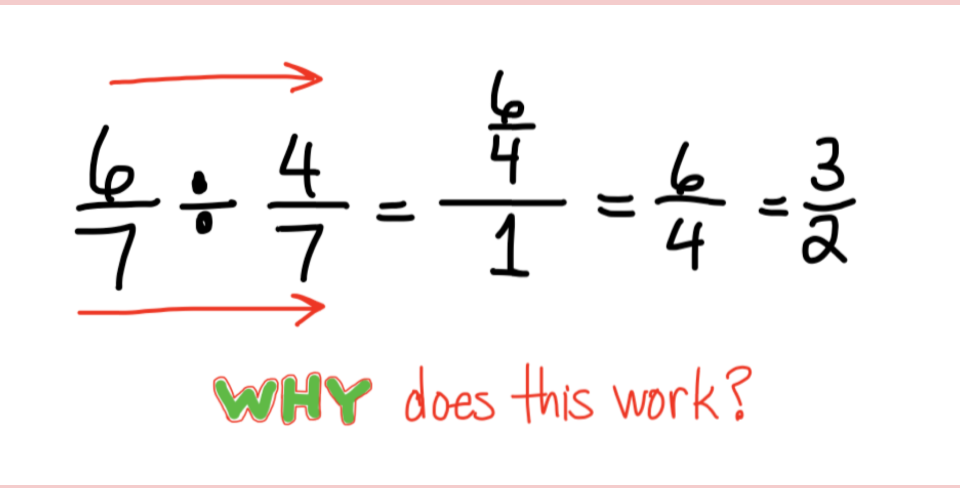
Nice! The powerful realization of identity properties a*1=a, then a/a=1, a not equal to 0 really stands out in these explorations and examples.
Excellent – repetitive reinforcement (1 seventh … so 3 sevenths etc)
and the use of the powerful strategy of patterns identification
which for me is the essence of all knowledge.
This is a very good tutorial in learning how to divide fractions. For me, the standard rule of dividing fractions is very important to be understood deeply to avoid confusion. The rule state that you have to invert the divisor fraction and apply the rule of multiplication of fraction. This means that you need to understand first the rule of multiplication of fraction. If there is doubt in the answer, I think fraction solver from https://www.fractioncalc.com/fraction-solver is a good reference.