I’ll bet you are wondering two things:
- What does the title mean?
- What the heck is a nutria?
Today I did a demonstration with a wonderful 6th grade class. We were comparing and ordering rational numbers. I grabbed this lesson from Open Up Resources. (It is an amazing free curriculum, but you might need to create an account to view it.)
The lesson is made up of two primary tasks, but we only managed to complete Task 1 during our lesson.
Task 1:
We used this set of cards. Students worked in pairs to sort the cards. First they sorted Set 1 (just positive numbers), then they sorted Set 2 (negative numbers).
Task 2:
If M is -15, what are the other values?
If N is -0.4, what are the other values?
We did not do Task 2 because we learned that students do not have an image pop into their brain when they see a particular fraction.
For example, 2.5, \(\frac{9}{8}\), and \(\frac{8}{3}\) were especially mysterious to students.
I used the example of APPLE versus NUTRIA. When I write the letters APPLE on the board, students likely had an image of an apple immediately pop into their brains. Perhaps it was a green apple or a red apple. Or perhaps it was an image of the apple pie grandma always makes for Christmas dinner. Regardless of the actual image, every student had an image pop into their brains when I wrote APPLE.
In contrast, I wrote NUTRIA on the board. Students could accurately read the word…but no image popped into their brain. Even after I briefly described a nutria as a pig-sized rodent, students still had no image pop into their brain.
This is what fractions are like!
Fractions are like nutria.
Sure students can correctly say “eight thirds” when they see \(\frac{8}{3}\), but no image pops into their brain. Our task is to teach students how to visualize \(\frac{8}{3}\)…just like they can visualize an apple.
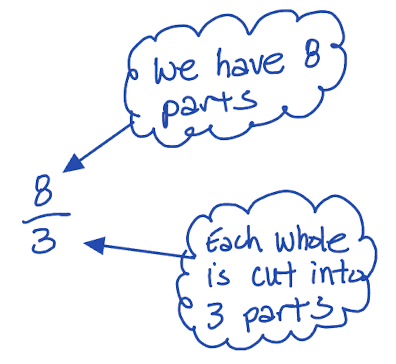
Let’s start with the meaning of the fraction \(\frac{8}{3}\).
The denominator tells us the number of equal parts of make one whole.
The numerator tells us the number of equal parts we have.
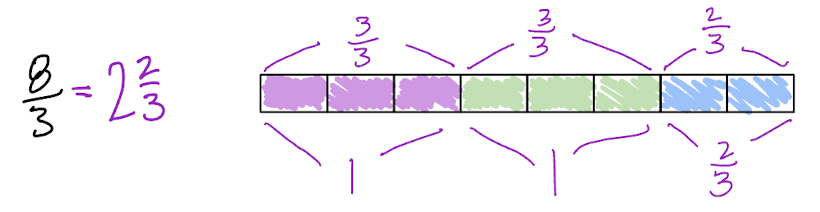
Now that students know what a fraction means, they might think of a tape diagram…
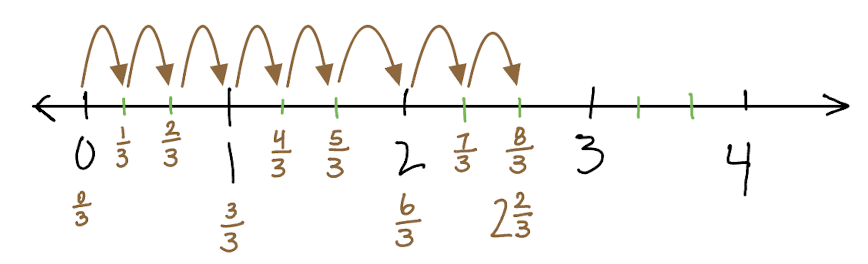
Or they might think of a number line…
It is okay that \(\frac{8}{3}\) might evoke different images in the minds of each student, the important thing is that each student needs to have a picture pop into their brain when they see a fraction.
If you want to learn more about how to use visual representations to teach ALL mathematics, please feel free to contact me at dhabecker@mcoe.org
.
.
.
.
.
By the way. If you haven’t already Googled it, here is an image of a nutria…
Now you have an image in your mind!