As a math coach who serves schools in multiple districts, I need to be clear on what I am aiming for during my coaching. What am I helping the teacher to do or learn or improve upon? I’ve decided my focus is to support teachers implement AMBITIOUS math instruction for their students.
Ambitious instruction deliberately creates an environment in which all students, regardless of ethnicity, race, socio-economic status, and gender, develop a deep and profound understanding of the content and are confident problem-posers and problem-solvers. There is ample evidence that students exposed to this sort of instruction make great progress in closing the achievement gaps that exist between categories of students.[2] Additionally, ambitious instruction requires that all students have equal opportunities to access rigorous grade-level curriculum. Simply by ensuring this access to high-quality curriculum, growth in student achievement increases by two months in a single year.[3]
Almost by definition, ambitious instruction is likely to be very different from current practice in classrooms. This is because, as Stigler and Hiebert put it, teachers follow a cultural script for teaching that is so ingrained in their pedagogical DNA that they don’t even know they are following a script.[4]
To improve instructional practices in the classroom, we must first understand the cultural script that we are following, the ramifications of that script on our students, and then we need to have a framework of instructional practices that are pieced together to create a new, more effective, cultural script for ambitious instruction.
The Merced County Office of Education Math Team has such a framework called the Math Hierarchy of Needs.
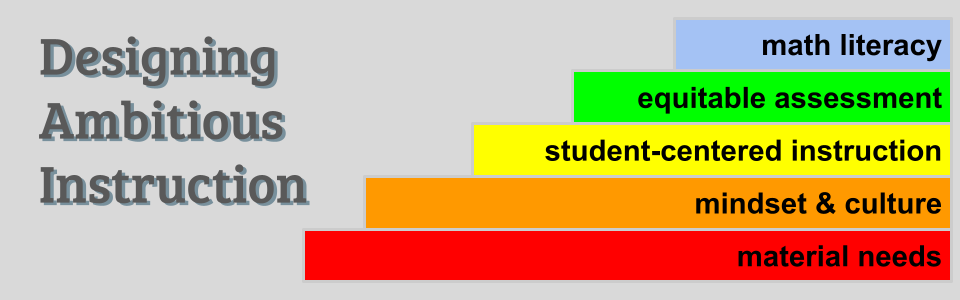
Math Hierarchy of Needs
Our vision is informed by the work of Abraham Maslow and his hierarchy of needs. Using his hierarchy as a model, we have created a mathematics hierarchy that guides our work in Merced County and acts as a roadmap for achieving our vision of creating empowered and confident problem-posing and problem-solving students.
In the same way that Maslow’s Hierarchy of Needs is a roadmap for how a person might experience the joy of experiencing self-actualization, with needs lower down in the hierarchy being satisfied before individuals can attend to needs higher up, the Math Hierarchy of Needs is a roadmap for how teachers and leaders might guide students towards becoming mathematically literate humans.
The hierarchy consists of five layers:
- material needs
- mindset and culture
- student-centered instruction
- equitable assessment
- mathematical literacy
Each layer consists of a plethora of things a district can choose to focus on with respect to their goals, personnel, resources, and strengths. Lower layers are not intended to be prerequisites before beginning work higher up the pyramid, but the layers in their entirety do tell a coherent story of an ambitious mathematics system. Ambitious, high-quality instruction is achieved when students fully experience each of the layers in the hierarchy on a regular basis.
Material Needs
Every student has a teacher with appropriate mathematics content knowledge and the knowledge for teaching mathematics. Math lessons are rooted in a solid understanding of grade-level standards through rigorous, high-quality curriculum and meaningful tools.
In Maslow’s hierarchy, the bottom layer addresses the physiological needs such as breathing, food, water, shelter, etc. Without fulfilling these needs a person will have little chance of thriving and advancing to the next level. In the Math Hierarchy of Needs, the bottom layer is called Material Needs.
Material Needs begins with the knowledge that for students to develop a deep understanding of mathematics they must experience a steady stream of effective math teaching practices. Building on Deborah Loewenberg Ball’s 30-year study of effective math teaching practices, powerful instruction requires teachers to have a specialized type of knowledge called Mathematical Knowledge for Teaching (MKT). MKT includes abilities such as analyzing the student thinking that led to an incorrect answer, identifying the mathematical understanding a student does not yet have, and deciding how to best represent a mathematical idea so that it can be understood by students.
Teachers need to have strong mathematics content knowledge for the purpose of making mathematics accessible for students. More than arriving at the correct answer, however, teachers need to know how to use concrete manipulatives, pictorial representations, and numbers and symbols to illustrate WHY the answer is what it is…not just HOW to get the answer.
Teachers also need a deep understanding of how students learn mathematics. For a given math concept, which visual representation might provide the biggest bang for the buck? Is there a solution strategy that might support students beyond just the current math concept, but also scales up to subsequent topics.
Lastly, teachers must have at their disposal instructional strategies that promote thinking, reasoning, and making sense of mathematics. There are a variety of such strategies: Thinking Classrooms, 5 Practices, Teaching through problem-solving, and Three-Part Lessons are examples. (More on this in Student-Centered Instruction.)
Mindset and Culture
Every student is immersed in a mindset and culture that intentionally communicates that all students can learn math at high levels while being responsive culturally and personally in a learning environment that considers each and every student’s unique background, experiences, cultural perspectives, traditions, and knowledge. Mistakes in mathematics are normalized. Students regularly experience high-quality, grade-appropriate lessons and assignments.
Once the material needs of students have been satisfied, students need to be immersed in a mathematical culture that supports them in taking risks and productively struggling with rigorous mathematics. This is the purpose of the mindset and culture layer. Students are provided the safety and security that declares all students are capable of learning rigorous mathematics and that mistakes are normalized as a necessary components of mathematics achievement.
Instrumental in the mindset and culture layer is students’ access to rigorous grade-level mathematics. The Opportunity Myth gives clear direction regarding the incredible growth in student achievement when students have access to grade-appropriate assignments, stronger instruction, deeper engagement, and higher expectations.[5] For example, students who started the year behind grade level and were provided access to stronger instruction and grade-appropriate assignments closed gaps in student achievement by more than seven months! Moreover, teacher expectations for students’ success with grade-level content is one of the strongest predictors of student growth.
Providing students with unfettered access to grade-level content requires teachers to create a culture for transforming mathematics learning. From Boaler’s Unlocking Children’s Math Potential, five research-informed practices are provided that create an environment in which such a culture will flourish.[6]
- All teachers demonstrate an unwavering belief that all students can learn mathematics at high levels.
- Support teachers and students in developing a growth mindset and ensure that the school system communicates a belief in growth mindset through its course pathways and student grouping practices
- Utilize “open” problem-solving opportunities that emphasize mathematics as a sense-making endeavor rather than merely an answer-getting endeavor.
- De-emphasize speed and establish mathematics as a subject that values depth of thought, insight, and creativity
- Teacher messaging and feedback to students that support a growth mindset rather than a fixed mindset
Student-Centered Instruction
Every student regularly experiences instruction that is student-centered and is designed to maximize students’ use of language. Lessons create space for students to participate in discourse to promote conceptual understanding, which then leads to procedural fluency, problem-solving, and application.
We subscribe to the commonly held belief amongst the education community that the person in the classroom who is doing the talking is probably the one who is doing the learning. In many typical classrooms, teachers are doing most of the talking, which means the students are learning far less than they otherwise could.[7] In response, classrooms need to be places where students are active participants in their own learning who regularly participate in academic discourse with their peers.
To provide the type of student-centered instruction necessary for students to become mathematically literate, the teacher will use instructional strategies that are unlike the typical classroom instruction of the past. We begin with the premise that students need to do most of the talking. In a typical classroom, teachers do 70% to 90% of the talking; and when students do speak it is generally limited to short one- or two-word answers. Student engagement is at its lowest when teachers are talking. On the flip side, however, student engagement and comprehension improve when they are the ones doing most of the talking.[8]
When student discourse is commonplace students are more likely to experience the three aspects of rigorous mathematics: conceptual understanding, procedural fluency, and application.
Conceptual understanding is the comprehension of mathematical concepts, operations and relations. Students with conceptual understanding know more than isolated facts and methods. Students see the connections among concepts and procedures and can give arguments to explain why some facts are consequences of others. This goes beyond memorizing procedures or individual facts to a focus on sense-making. Teaching conceptual understanding enables students to understand a concept from multiple perspectives and look for patterns that can help them understand future problems.[9] Developing conceptual understanding also leads directly to students more effectively learning standard algorithms.[10]
Standard algorithms are one component of procedural fluency. Procedural fluency refers to knowledge of procedures, knowledge of when and how to use them appropriately, and skill in performing them flexibly, accurately, and efficiently. Students also need to know reasonably efficient and accurate ways to add, subtract, multiply, and divide multi-digit numbers, both mentally and with pencil and paper. Students need to see that procedures can be developed that will solve entire classes of problems, not just individual problems.[11]
Student-centered classrooms also provide students with opportunities to apply their conceptual understanding and procedural fluency through problem-solving activities in which the solution method is not immediately obvious. The standards call for students to use math in situations that require mathematical knowledge. Correctly applying mathematical knowledge encourages students to develop a solid conceptual understanding and procedural fluency. To engage in application:
- Students need opportunities to apply mathematical knowledge and/or skills in a real-world context.
- Materials should promote activities that call for the use of mathematics flexibly in a variety of contexts in both routine and non-routine problems.
- Students are given opportunities to use math to make meaning of and access content.
Equitable Assessment
Every student is regularly and humanely assessed in order to have understanding of their own growth and to receive productive feedback for next steps in learning. Students use the feedback to know where they are in their learning, assess any misconceptions that need to be addressed, and then use the results to drive the next level of learning.
Assessing students in mathematics is a crucial component of the education system, as it helps teachers and students identify areas where students are excelling or struggling. However, it is equally important to conduct assessments in a humane way that takes into account the individual differences and unique circumstances of each student. This means that teachers should avoid solely relying on standardized tests and instead adopt a variety of assessment methods that are tailored to meet the needs of each student.
One of the main benefits of assessing students in a humane way is that it can help boost their confidence and motivation. If students feel like they are being assessed in a fair and personalized way, they are more likely to engage with the material and feel a sense of ownership over their learning. Conversely, if students feel like they are being judged solely based on their test scores, they may become discouraged and lose interest in the subject.
Another important reason to assess students in a humane way is that it can help address issues of equity and accessibility in mathematics education. Standardized tests are often biased towards certain groups of students, such as those from more privileged backgrounds or those who are proficient in English. By adopting a more personalized approach to assessment, teachers can ensure that all students have an equal opportunity to succeed in mathematics and that their unique strengths and challenges are taken into account.
Mathematical Literacy
Every student has the opportunity to analyze, reason, and communicate ideas effectively as they pose, formulate, solve, and interpret mathematical problems.
This is the goal for students: mathematical literacy. The entire purpose of the Mathematics Hierarchy of Needs is to provide the framework for teachers, schools, and districts to create math communities where students flourish as confident problem-posers and problem-solvers. The Organization for Economic Co-operation and Development (OECD) best describes mathematical literacy as
“an individual’s capacity to formulate, employ and interpret mathematics in a variety of contexts. It includes reasoning mathematically and using mathematical concepts, procedures, facts and tools to describe, explain and predict phenomena. It assists individuals to recognise the role that mathematics plays in the world and to make the well-founded judgements and decisions needed by constructive, engaged and reflective citizens.” (OECD, 2018, p. 67)
Here we provide a simple bird’s eye view of the hierarchy…
Let’s take a look at the mathematics hierarchy of needs and some practical examples for each layer of the pyramid. When trying to create an ambitious mathematics program for a school site or an entire district, each of the layers must be fully addressed for students to become confident problem-posers and problem-solvers. In other words, students who are mathematically literate.
Each layer of the hierarchy is non-negotiable. However, what a site or district does to satisfy the needs of any particular layer depends on the unique strengths and human resources available to them.
We offer high-quality professional development designed to support every site and district to satisfy each layer.
Initial training would focus on the specified initiative. For most training, the session will include classroom, physical or virtual, demonstrations where students participate in the strategy being covered and teachers observe. Subsequent to the demonstration, teachers will have the opportunity to debrief, and in some cases, have the opportunity to utilize deliberate practice within the training ahead of introducing into their own teaching practice in the classroom.
Equitable Instruction
Despite our vision that every student is empowered by the opportunities mathematics affords, the evidence is compelling that traditional (typical) instructional practices result in fewer opportunities to learn in mathematically powerful spaces for children who are identified as Black, Latinx, Indigenous, multiple language learners, economically disadvantaged, with disabilities, along with other marginalized learners.[12]
The Math Hierarchy of Needs provides a framework for designing a mathematics instructional ecosystem in which learning opportunities are equitably distributed (Lampert & Graziani, 2009; NCTM, 2000)[13]. In other words, students who are multiple-language learners, in special education, and/or are members of historically underserved communities should have the same access as the general population to the empowering opportunities mathematics affords.
Some foundational components of the hierarchy for establishing ambitious math instruction with equitable results are:
- Student access to high-quality grade-level mathematics curriculum (Material Needs)
- Instruction that is engaging, affirming, and meaningful for students (Mindset & Culture)
- Mathematics lessons that regularly require students to interact with and employ the use of the eight standards of mathematical practice that strengthen student identity and agency. (Student-centered Instruction)
- Provide targeted intervention and support within the typical lesson rather than in a “pull-out” environment. (Equitable assessment)
The MCOE Math Team is keenly aware that instruction guided by the Math Hierarchy of Needs results in equitable instruction that positively predicts mathematics achievement on cognitively demanding assessments such as California Assessment of Student Performance and Progress (CAASPP).[14]
.
.
.