Sprouts is a paper-and-pencil game that can be enjoyed simply by both adults and children. Yet it also can be analyzed for its significant mathematical properties. It was invented by mathematicians John Horton Conway and Michael S. Paterson at Cambridge University in the early 1960s. Setup is even simpler than the popular Dots and Boxes game, but game-play develops much more artistically and organically.
Rules
The game is played by two players, starting with a few spots drawn on a sheet of paper. Players take turns, where each turn consists of drawing a line between two spots (or from a spot to itself) and adding a new spot somewhere along the line. The players are constrained by the following rules.
- The line may be straight or curved, but must not touch or cross itself or any other line.
- The new spot cannot be placed on top of one of the endpoints of the new line. Thus the new spot splits the line into two shorter lines.
- No spot may have more than three lines attached to it. For the purposes of this rule, a line from the spot to itself counts as two attached lines and new spots are counted as having two lines already attached to them.
In so-called normal play, the player who makes the last move wins. In misère play, the player who makes the last move loses. Misère Sprouts is perhaps the only misère combinatorial game that is played competitively in an organized forum.
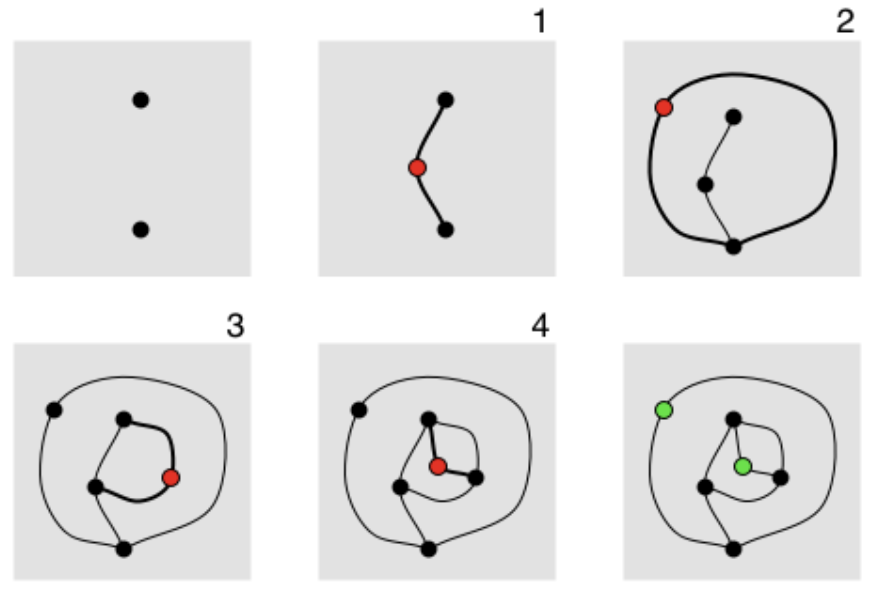
The diagram shows a 2-spot game of normal-play Sprouts. After the fourth move, most of the spots are dead–they have three lines attached to them, so they cannot be used as endpoints for a new line. There are two spots (shown in green) that are still alive, having fewer than three lines attached. However, it is impossible to make another move, because a line from a live spot to itself would make four attachments, and a line from one live spot to the other would cross lines. Therefore, no fifth move is possible, and the first player loses. Live spots at the end of the game are called survivors and play a key role in the analysis of Sprouts.
Here is a Google Slides version of Sprouts
.
.
.
