Using the Empty Number Line

When I teach new mathematical concepts to my students, I always try to use some sort of visual model to make the learning easier. No duh! But what I have noticed is that over the years I have collected an odd assortment of models to teach everything without any theme to all the models. The model for teaching fractions looks nothing like the model for integers.

By the end of the school year, the models that were intended to make learning mathematics easier began to get jumbled in the minds of my students. No good.

Then came the empty number line, which has become a unifying model that can work in a variety of different math concepts.

The empty number line is simply a line without regular intervals and without the zero being indicated unless needed. Students can use the number line to record their thoughts for solving the problem. Below are small examples of how the empty number line can be used in various math concepts:

Using the empty number line to add whole numbers:

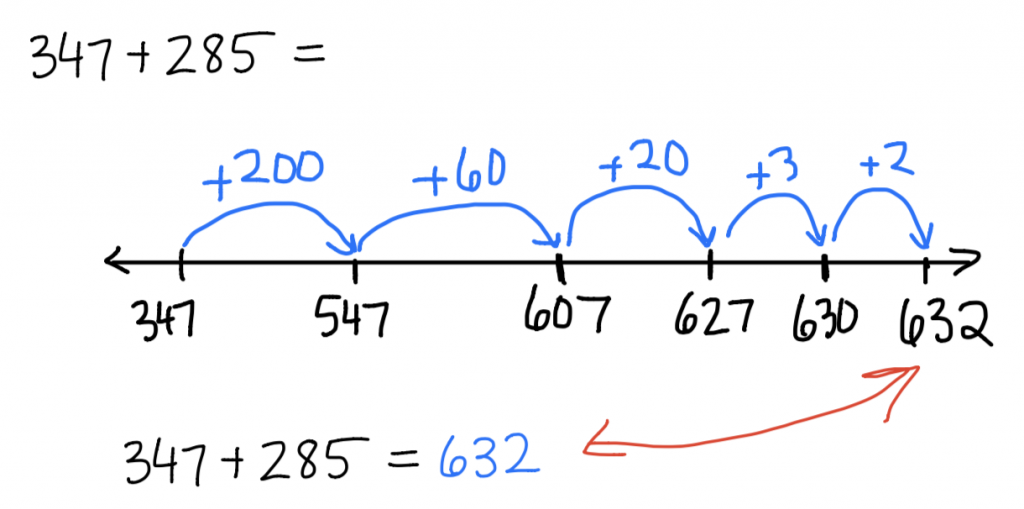
Starting on the empty number line at 347, we make a series of hops that have a sum of 285. Where we end up on the number line is the solution to 347 + 285.

Using the empty number line to subtract whole numbers:

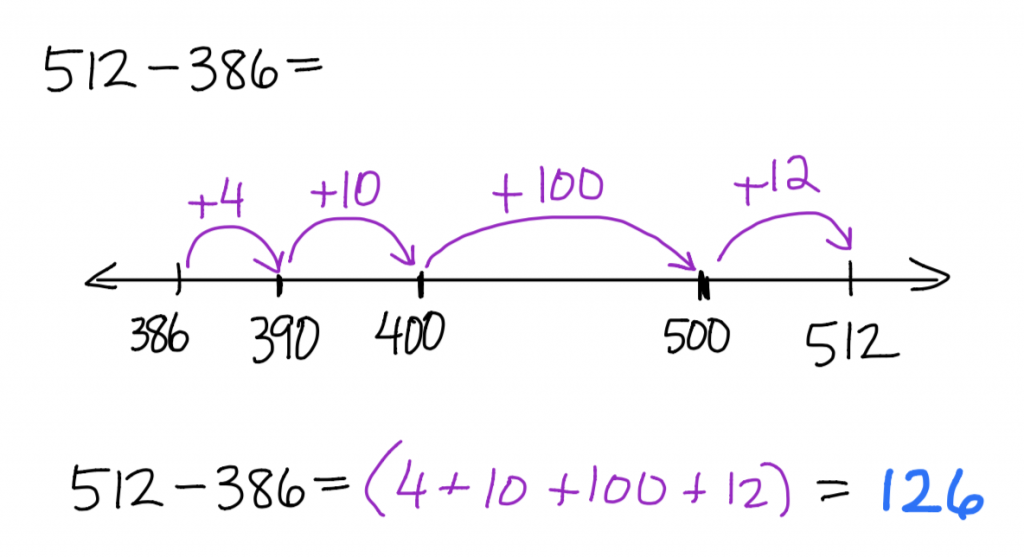
To model subtraction, you begin by placing 386 and 512 on the empty number line. Then using any series of hops, find the distance from 386 to 512. In the example above, 4 is added to get to 390. Then 10 is added to get to 400. Then 100 is added to get to 500. Finally, 12 is added to get to 512.

Summing the hops from 386 to 512 gives us the difference of 512 and 386.

4 + 10 + 100 + 12 = 126

The REAL power of using the empty number line is that it builds number sense in the students. It causes the focus to shift from the students trying to memorize an algorithm to students developing number sense while making up their own series of hops along the number line.

The awesome power of empty number lines becomes very apparent with subtracting fractions.

Using the empty number line to subtract a mixed number from a whole:

Example 1

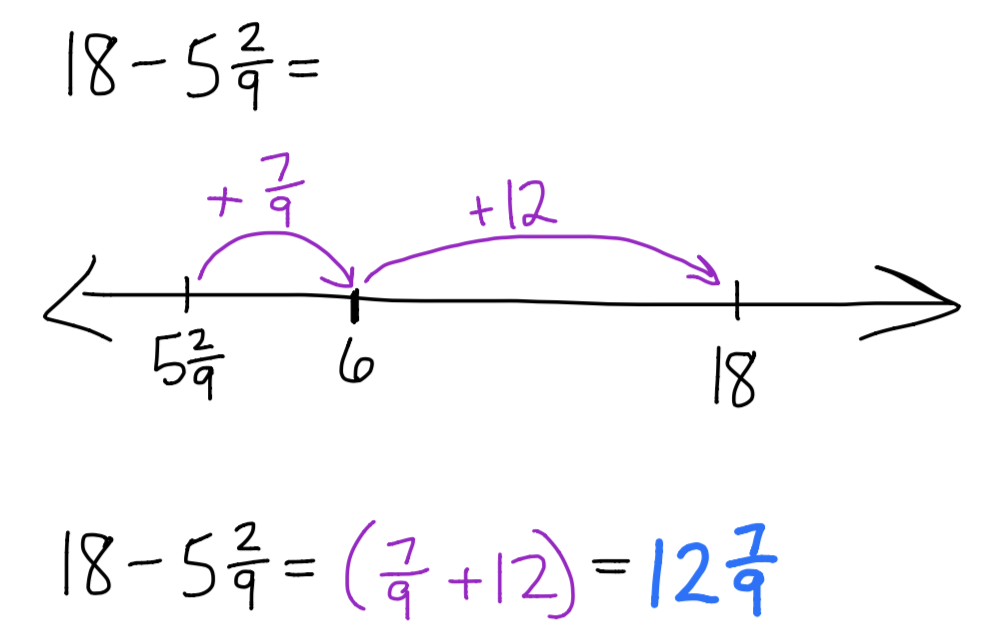
To subtract, we need to think of finding the distance between the two numbers. In the above example, we place \(5\frac{2}{9}\) and 18 on the number line and then use any series of hops to find the distance from one to the other. The drawn number line shows a hop of \(\frac{7}{9}\) and a hop of 12. This means the difference is\(12\frac{7}{9}\).

Example 2

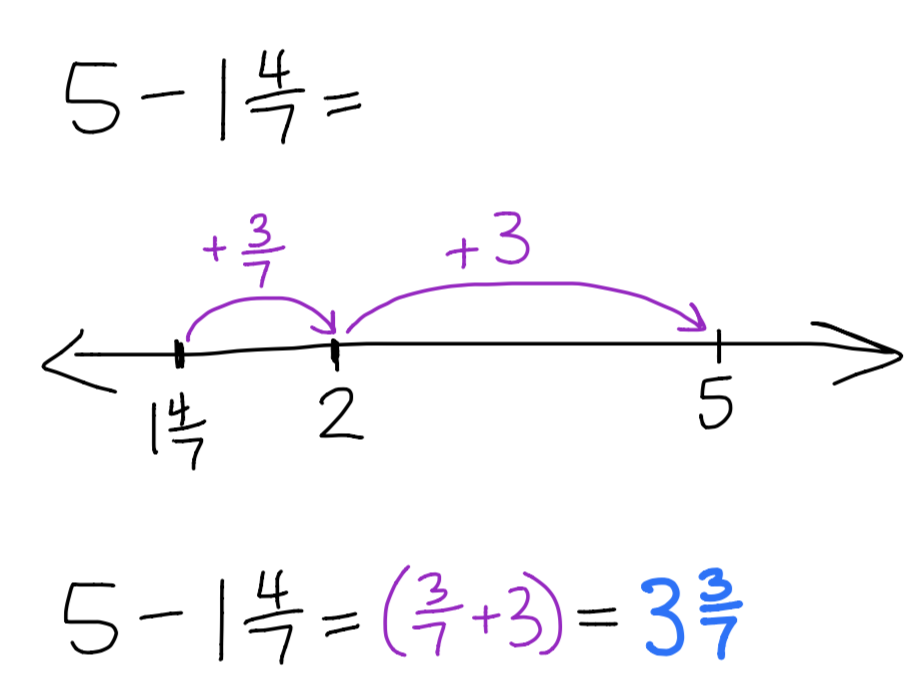
Using the empty number line to subtract mixed numbers with the same denominator:

Example 1

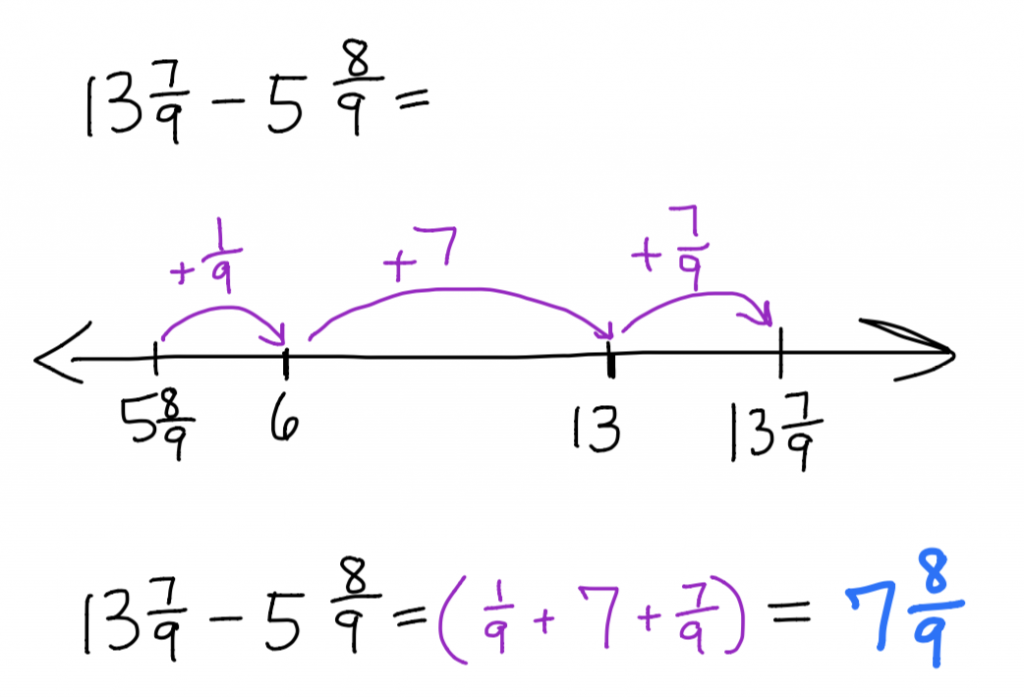
After placing \(5\frac{8}{9}\) and\(13\frac{7}{9}\), we can use three hops to find that the distance is\(7\frac{8}{9}\).

Example 2

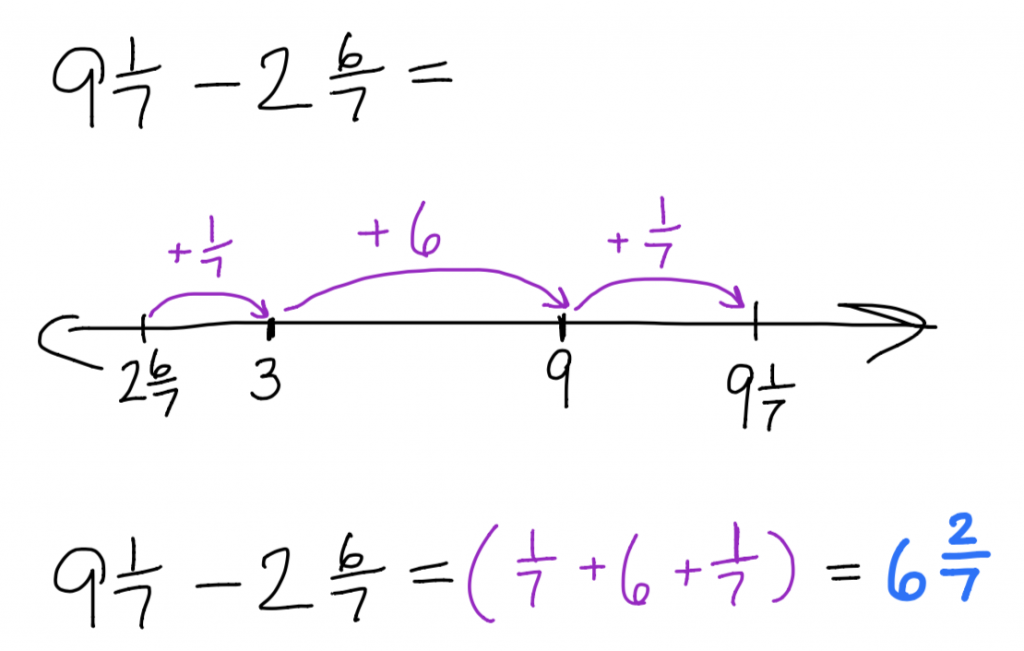
Using the empty number line to subtract mixed numbers with different denominators:

Example 1

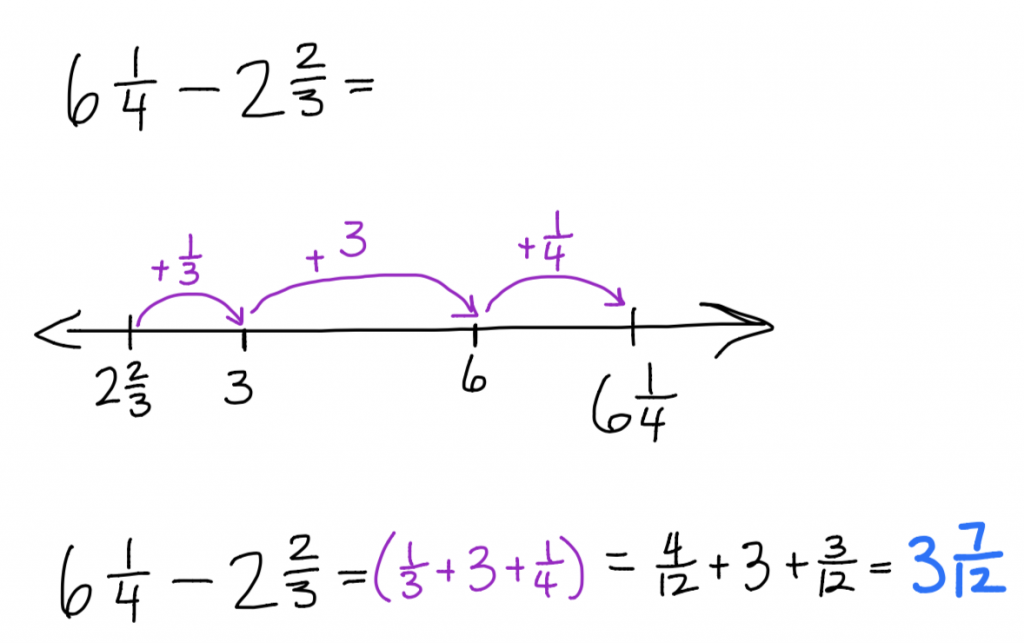
In this example we can use three hops to find the distance from\(2\frac{2}{3}\) to\(6\frac{1}{4}\). However, we need to get a common denominator to find that the difference is\(3\frac{7}{12}\).

If you have any questions or comments on using the empty number line, please speak up!

.

.

.