Recently, I have found myself vociferously advocating for more teachers to use number disks when teaching the four operations of whole numbers: addition, subtraction, multiplication, and division. Clearly my excitement for number disks has not yet rubbed off onto all the teachers I work with, because today I received the following question:
Why are disks better than the 100 blocks, ten sticks, and ones cubes we have been using?
It is clear the teacher is a user of Base 10 blocks. It is reasonable to ask why, if Base 10 blocks work, then why should we also learn about number disks.
Here was my reply:
Hi there XXXXX!
Great question. At Grade K and Grade 1, we prefer using the Base 10 blocks you mentioned. During 2nd grade, however, we want to transition to using Number Disks. Here is why….
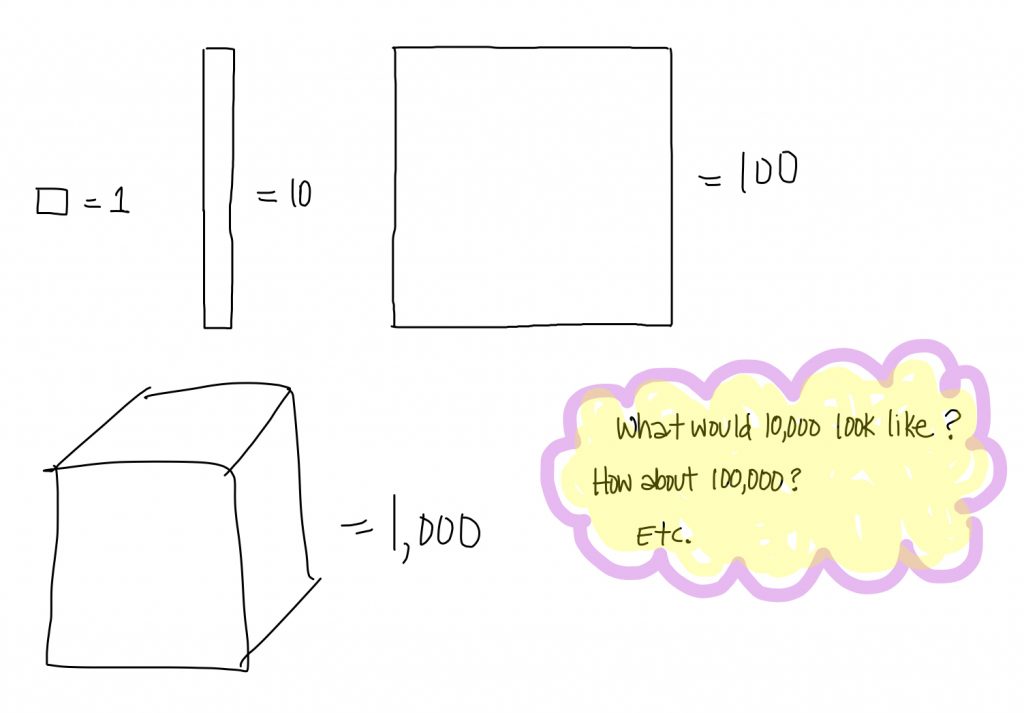
In 2nd grade students begin adding/subtracting within 1000. What would 1000 look like? To model a thousand, students would have to draw a cube, which is rather tricky. It gets worse in 3rd grade when students need to model beyond 1000, and then students in 4th grade will have to model up to 1,000,000! Within the Base 10 blocks, there is no useful geometric shape students can use to represent 10,000 or anything larger. With Number Disks, however, representing very large numbers becomes trivial.
It is essentially the same story with decimals. Only now, number disks become the preferred visual for very small numbers.
I hope this gives you food for thought!
That was my brief email. I hope it was okay. (Please give me additional food for thought!)
I’ll go into great detail for each of the operations…
ADDITION
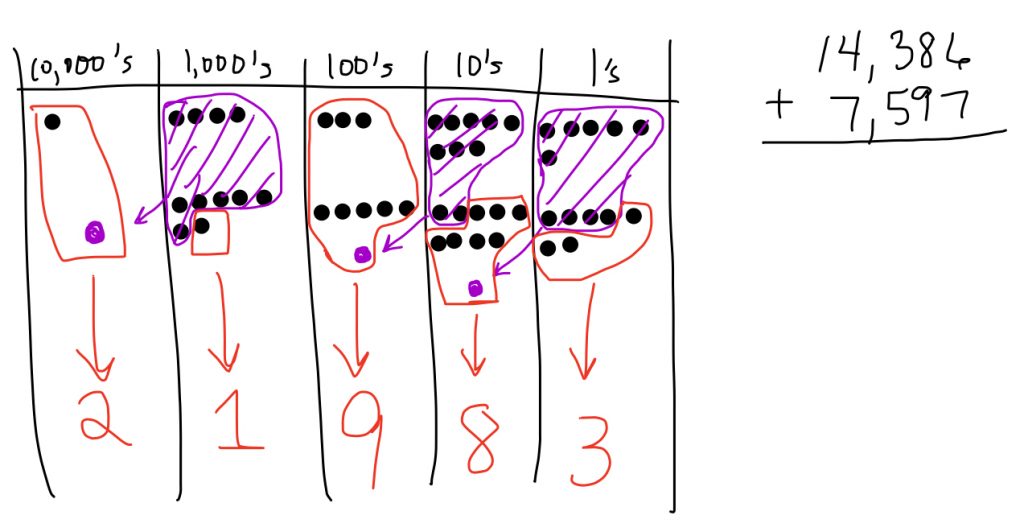
In my email response (above), I provided an example for 14,386+7,597, but I forgot to show the algorithm worked out. Here is what it would look like…
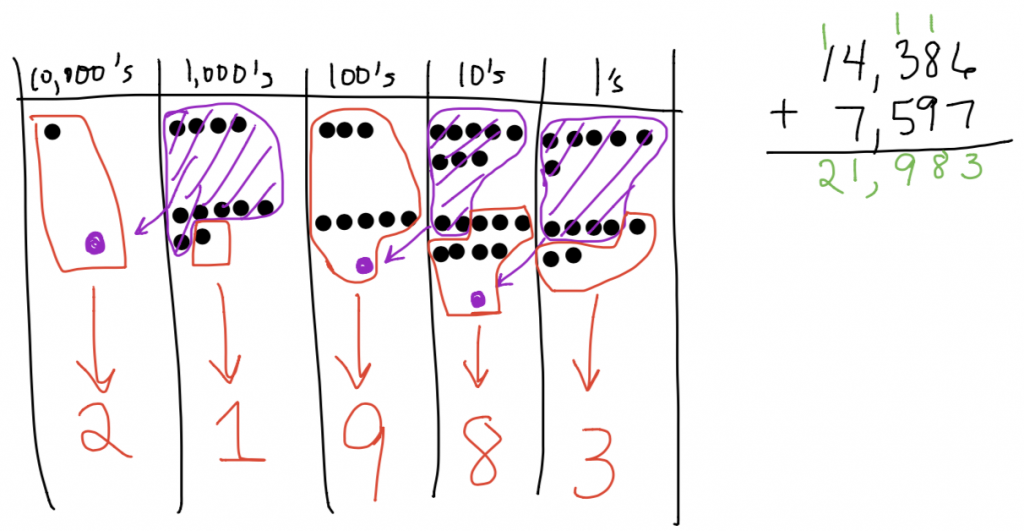
It amazes me how closely using the number disks mirrors the traditional algorithm. Try it yourself with 268 + 147.
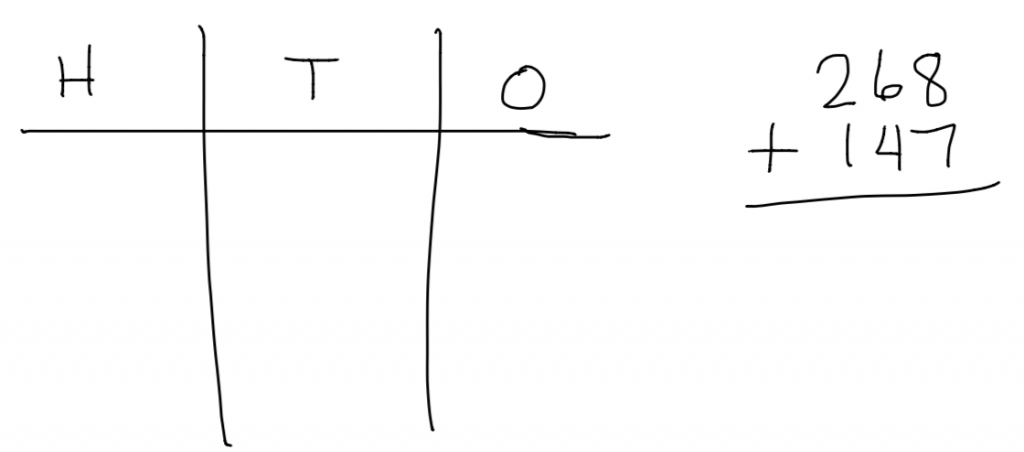
Once you’ve given it a try, check out my video to check your work.
SUBTRACTION
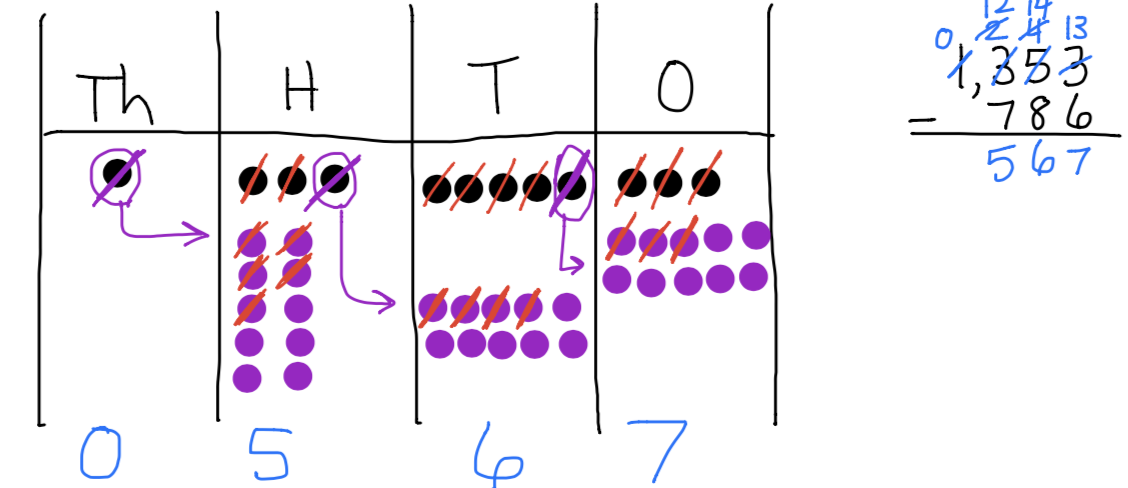
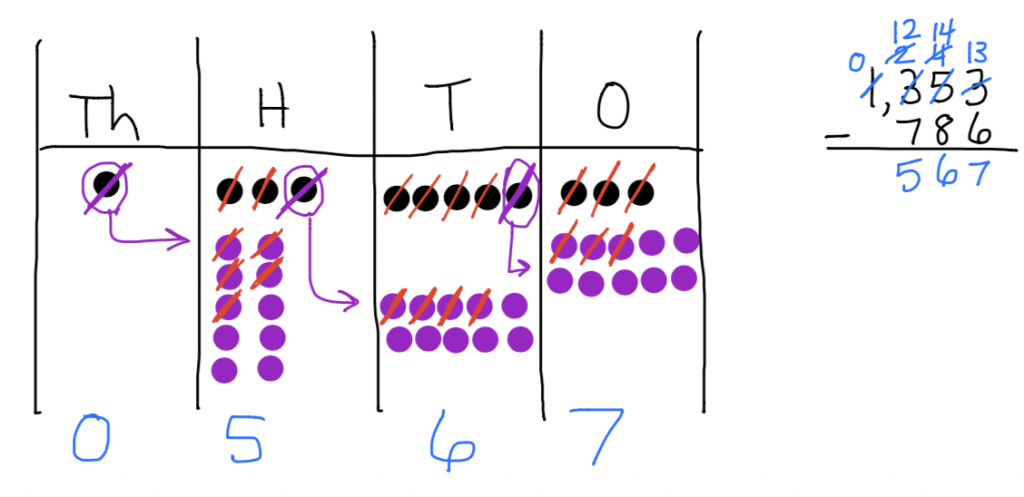
Here is another example that demonstrates how closely using number disks mirrors the traditional algorithm. In this case we are solving 1353 – 786.
Now give 326 – 159 a try.
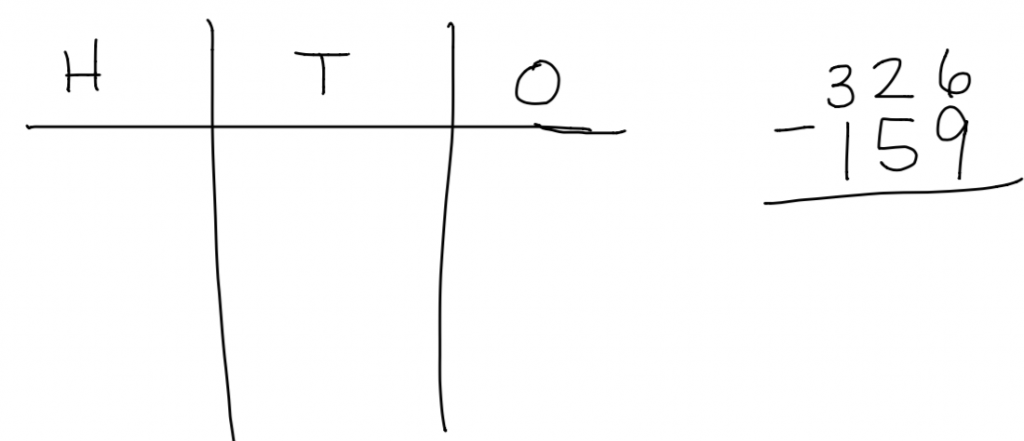
Watch my video to check your work.
MULTIPLICATION
Using number disks for multiplication is easiest when one of the factors is small…less than 15 or so. Problems like 1326 x 9 are perfect with number disks.
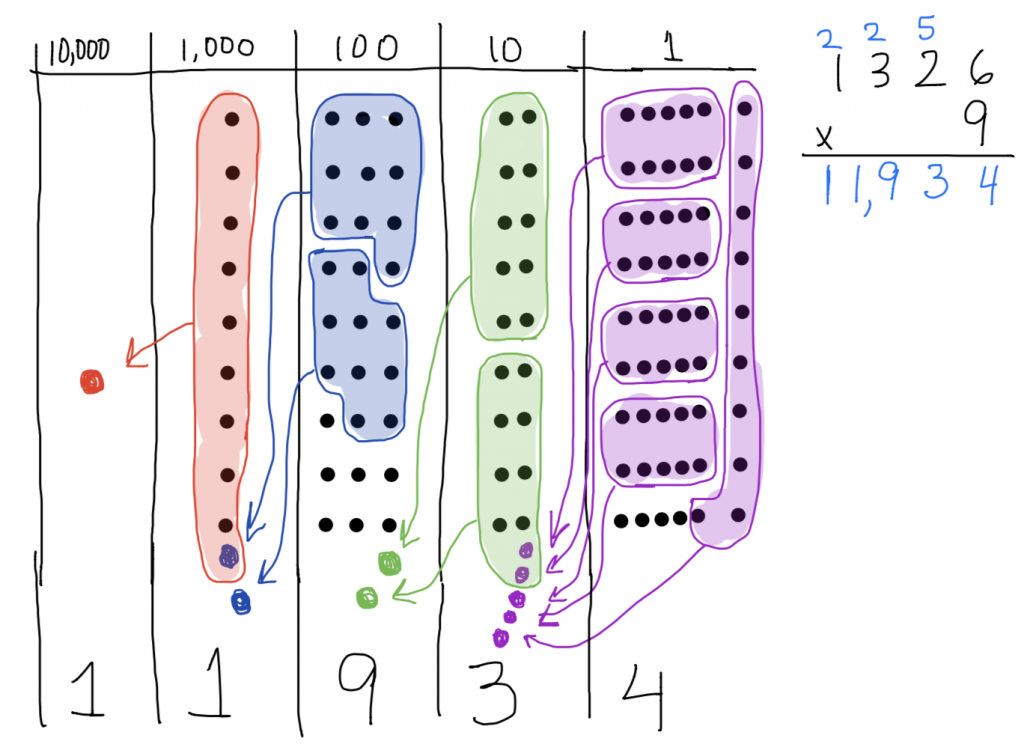
Now give 4 x 267 a try.
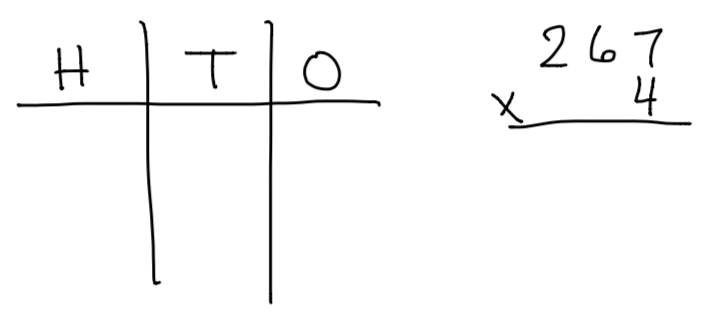
Watch my video to check your work.
DIVISION
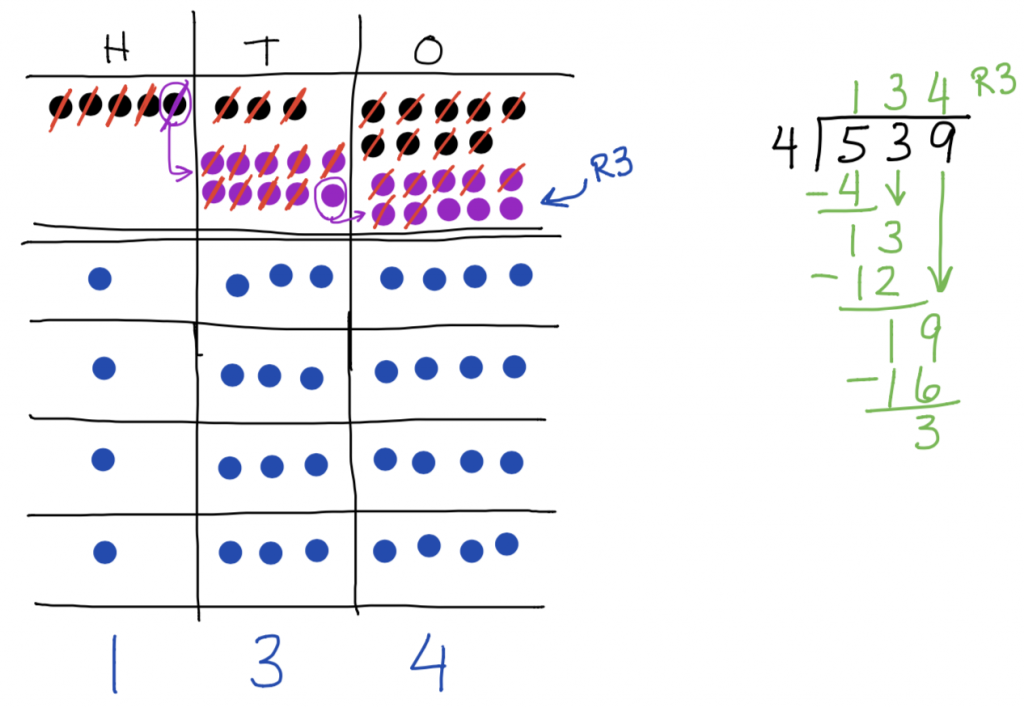
This is the one that number disks really show their power. Here is an example of the division problem 539 ➗4.
Now give 98 ➗4 a try.
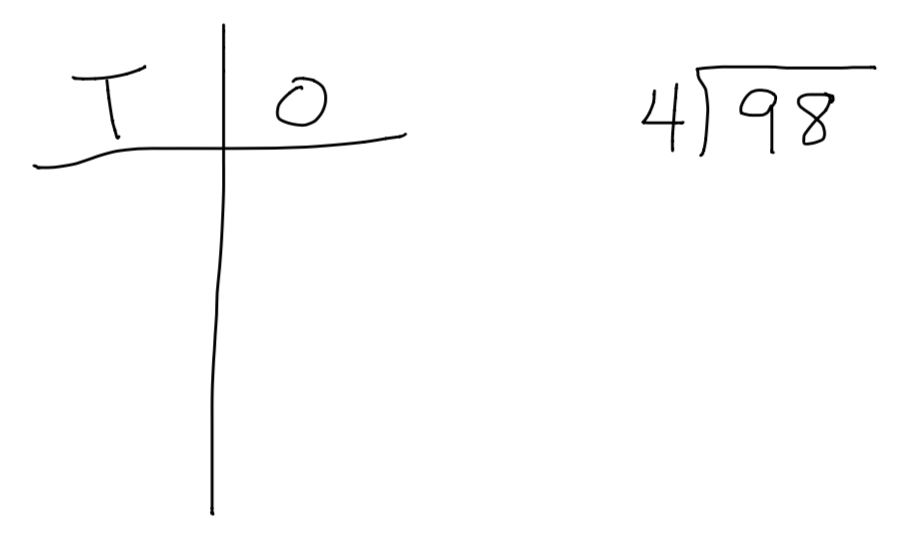
Watch my video to check your work.
Try number disks with your students. Let me know how it goes in the comment section below.