Fifteen years ago I thought I knew how to teach mathematics. At that point, I had been teaching mathematics at the secondary level for about thirteen years. I was a proud, card-carrying member of local and national mathematics organizations such as California Math Council (CMC), Bay Area Math Project (BAMP), and the National Council of Teachers of Mathematics (NCTM). I attended all their conferences and read all their periodicals. The key to successfully teaching mathematics, I thought, was to carefully and thoughtfully sequence the lessons just so, such that students would be gently guided along – as if on a tour through a museum – to all the various math concepts to be learned. With my perfectly crafted series of lessons, the students could not help but to learn the beauty and utility of the mathematics – as I saw it.
I no longer believe that the key to successfully teaching students mathematics is in discovering the perfect sequence of lessons. I was operating on the naive assumption that mathematics could be packaged, “ready-made, for the students to pick up, if only they had the will to do so”[1], and that “conceptual knowledge [could] be transferred from [me] to student” simply by finding a logical progression of lessons and delivering them with passion[2]. Rather, I have come to understand that – by knowing my students and having a general idea of their current mathematical knowledge – I can create a series of math experiences in which students interact with those experiences, add to their schema, and thereby “changing their ways of thinking”[3] and developing their own understanding[4].
Even though I had moved away from searching for that magical linear progression of math lessons, instead focusing on a more constructivist approach, I was still operating under the traditional paradigm of “I do. We do. You do.” Unsurprisingly, students continued to rely on me as the fount of all mathematical knowledge. My evolution toward constructivism took a major step forward as a result of the TIMSS 1999 Video Study, specifically episode JP3 – a Japanese eighth grade lesson on linear inequalities[5]. In this lesson the teacher guides students through a lesson that is best characterized as “You do. We do. I do.” The exact opposite of what I was accustomed to! The lesson began with the teacher introducing a word problem to be solved. Students worked alone or in pairs, grappling with the problem, making sense of it, and connecting it to prior lessons and concepts. After most students had solved the problem in some fashion, the teacher strategically selected some students to share their solution methods on the chalkboard. In looking at the strategies the students were sharing, it immediately became clear that the teacher was selectively choosing students to share methods with increasing levels of complexity. Each new method shared was more efficient and closer to the standard algorithm than the previous one. Lastly, the teacher wrapped up the lesson by comparing and contrasting each of the methods shared and then connecting them to the efficient algorithm.
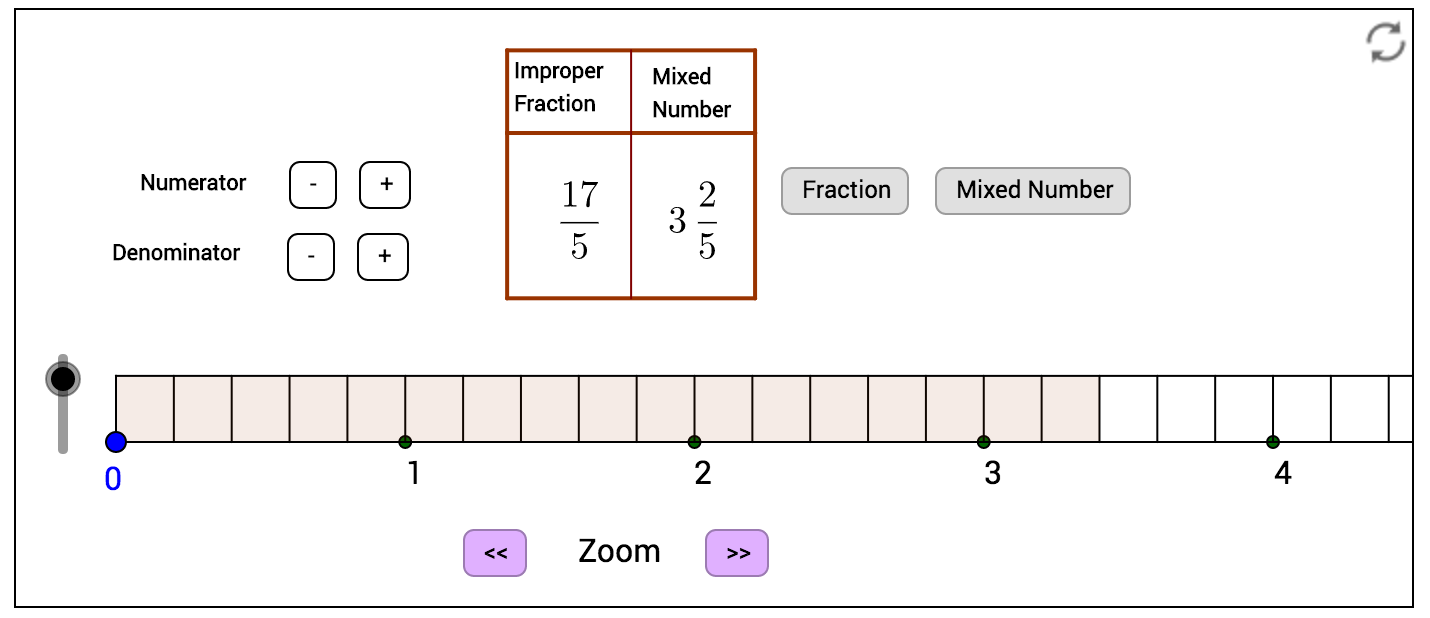Starting with “You do” provides students an opportunity to productively struggle with the math concept and develop their own understanding of the mathematics. With this in mind, I now regularly use Number Talks as a regular component of the mathematics instructional coaching that I do. In number talks, students develop their math understanding by sharing various solution methods which are grounded in conceptual understanding rather than on rote memorization of algorithms. Similarly, many of the GeoGebra applets I have created are designed to allow students to “play” with the mathematics, rapidly hypothesizing and prototyping in order to make sense of the underlying mathematical truth inherent in the applet. In this example, students dynamically create improper fractions and watch the change in the resulting picture and mixed number. This opportunity students to engage in sense-making (“You do”) creates opportunity for comparing and contrasting the various student hypotheses (“We do”), resulting in a deeper, constructivist-inspired math understanding that I connect to the standard algorithm (“I do”).
Wrapping things up
According to von Glasersfeld, mathematical understanding is not something that can be handed down from the teacher to the student like a baton in a relay race. Rather, the goal of the teacher is to create fertile ground – the opportunities and incentive[6] – which allow mathematical knowledge to grow amongst the students.
[1] “Ernst von Glasersfeld.” http://vonglasersfeld.com/180. Accessed 11 Apr. 2017.
[2] “Ernst von Glasersfeld.” http://vonglasersfeld.com/180. Accessed 11 Apr. 2017.
[3] “Ernst von Glasersfeld.” http://vonglasersfeld.com/180. Accessed 11 Apr. 2017.
[4] “Presentation by Grover J. (Russ) Whitehurst, Director, Institute of ….” https://ies.ed.gov/director/speeches2003/02_06/2003_02_06.asp. Accessed 11 Apr. 2017.
[5] “JP3 Solving Inequalities | TIMSS Video.” http://www.timssvideo.com/49. Accessed 11 Apr. 2017.
[6] “Ernst von Glasersfeld.” http://vonglasersfeld.com/180. Accessed 12 Apr. 2017.
sure here with prof dr mircea orasanu
“You do. We do. I do.” – That’s how the real world works as well. I think this a future-proof method for teachers.
Thanks for sharing this article with us!