As a math coach for the past 12 years or so, I notice a lot of students in 3rd and 4th grade you are still using their fingers to add two single-digit numbers together. Using fingers to “count on” an addition fact 7+ 5 for example, is perfectly fine in kindergarten or 1st grade, but too often I see students who do not advance to automaticity or immediate recall. In this post, I’ll walk you through my process for getting ALL students to know their addition facts.
What is fluency?
Let’s begin by quoting the CA Math Standards: “By end of Grade 2, know from memory all sums of two one-digit numbers.” (2.OA.2)
Notice the word is “memory” and not “memorized”. Knowing one’s addition facts from memory is the result of repeated experience working with the number facts in a variety of ways such that eventually the facts is known from memory. Learning facts through memorization denies students the opportunity to develop a deep understanding of the meaning of addition in the first place.
How is fluency developed?
Students need to progress through the different levels of mathematical reasoning. First students use counting strategies, but then they advance to additive thinking and using strategies.
Research tells us that students generally do not master their addition facts because traditional teaching approaches too often allows students to get stuck at Stage 2 without ever fully developing a set of strategies that students can use on their way towards fluency.
While we are happy any time a student can correctly say that 9 + 6 is 15. What the teacher REALLY is interested in is HOW the student arrived at 15. Was it through counting strategies? The use of an addition strategy? Or was it from recall?
We want recall.
At first glance there are 100 addition facts that students need to learn.
That’s a lot of things to memorize so we need to break these 100 facts into smaller chunks. We can immediately cut this in half by recognizing the commutative property. For example, 4 + 8 and 8 + 4 are really the SAME addition fact.
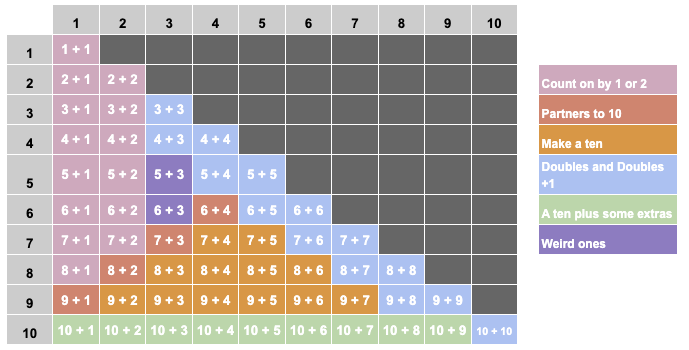
Now I provide explicit instruction to clearly and directly teach the four most important strategies. Here is the order I usually teach them and practice them…
- Count on by 1 or 2
- Partners to 10
- Make a ten
- Doubles and Doubles +1
As students are learning one of the addition strategies, I will give each student a four or five blank 3×5 cards for them to create flashcards for the facts they are having the most difficulty recalling.
How to make the cards:
- Front of card: write the addition problem (not the answer!)
- Back of card: write the answer AND show the strategy used.
Some students prefer visuals such as…
Towards the end of the process, each student will have their own unique set of flashcards with the answer and strategy on the back. Students should have at least a few cards from each of the four categories. However, you will want to emphasize cards for the Make a Ten strategy.
Later, while students are using their flashcards they can sort their cards based on the strategy they use to remember the fact.
Throughout the rest of the school year, I will occasionally ask students to take out their flashcards for retrieval practice, which involves the act of them trying to recall the answer from memory. Spaced practice involves distributing the flashcard practice over time. Retrieval and spaced practice have been studied a lot and have been shown to be highly effective in getting students to memorize their addition facts.
One additional thing I do to ensure my students become fluent with their addition facts is I allocate a tremendous amount of time for students to compare the different representations (ten frame, number line, number bond, etc.) and strategies (doubles, near doubles, make a ten, etc.) they prefer to use. This often comes in the form of a number talk or a problem string. In addition to sharing the answer, students are also invited to share how they see the problem in their mind. Were the numbers represented in a ten frame? Or a number line? Were the numbers doubling? Or were they breaking apart and reassembling as a ten plus some extras?
I hope this provides you a bit of a game plan for supporting your students’ addition fluency.
.
.
.