PROBLEM 1
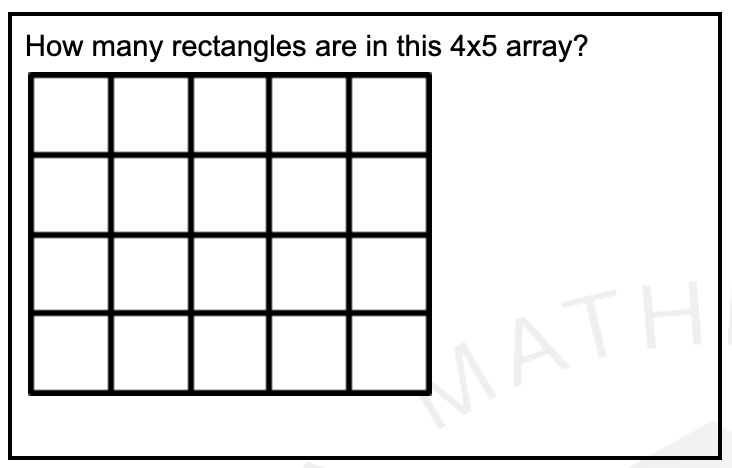
The key strategy on this problem is to be super precise with your counting. For example, by treating 1×2 rectangles as DIFFERENT from 2×1 rectangles, you will see some pretty awesome patterns.
Start by counting the 1-by’s and you will see there are 60 of them. You might also see a nice pattern.

Now count the 2-by’s to see that there are 45 of them. Do you see the pattern?
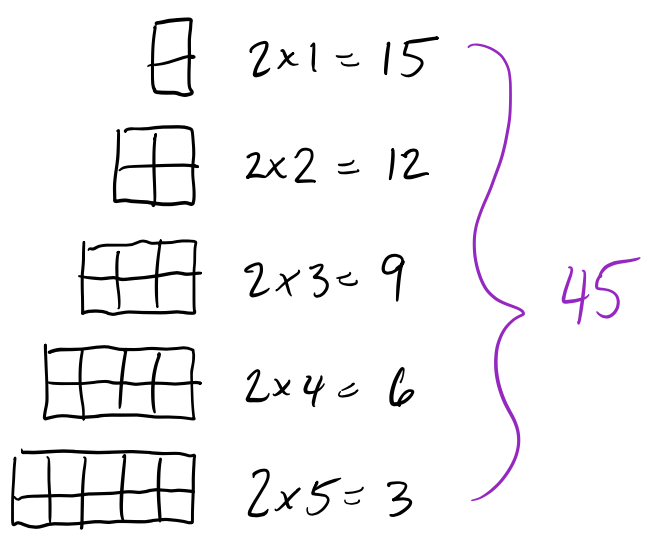
Now the 3-by’s and 4-by’s.
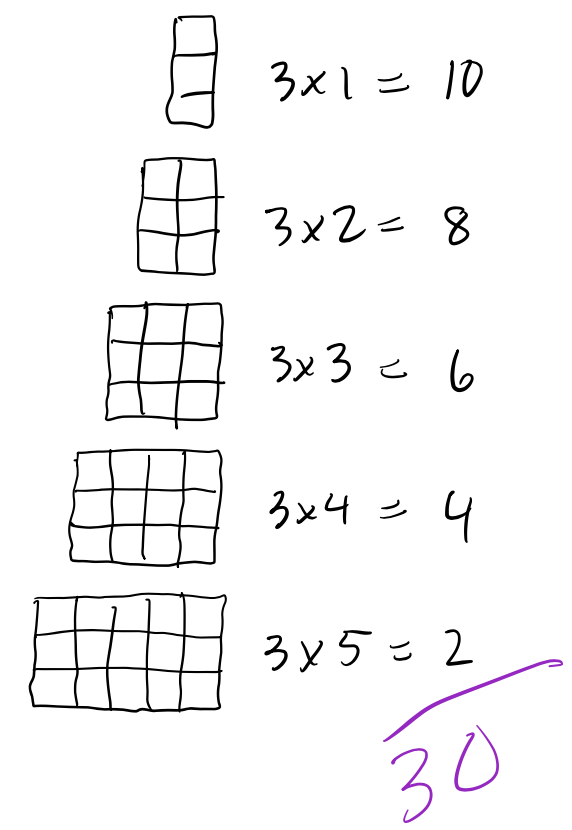
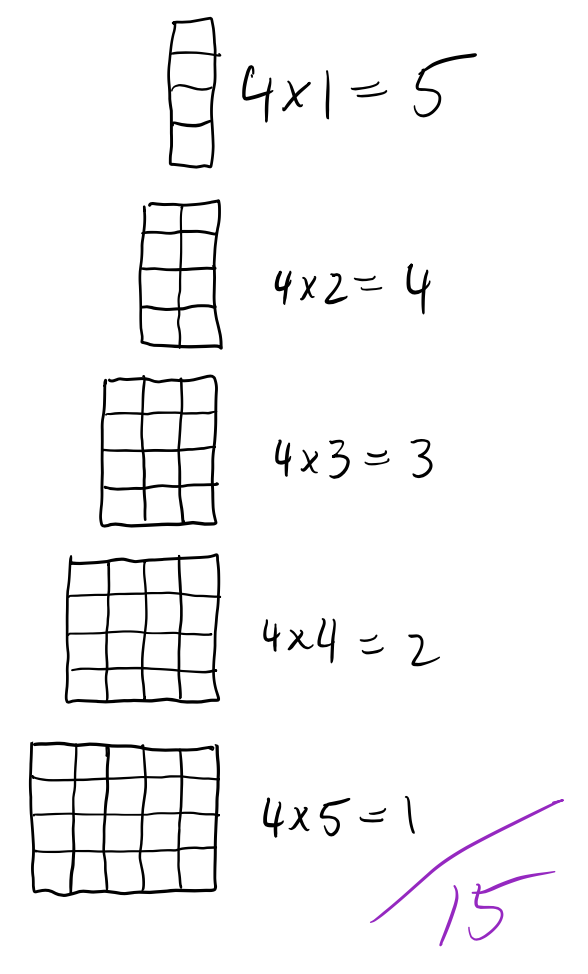
Adding up all the subtotals and we find there are 150 rectangles in the 4×5 grid!
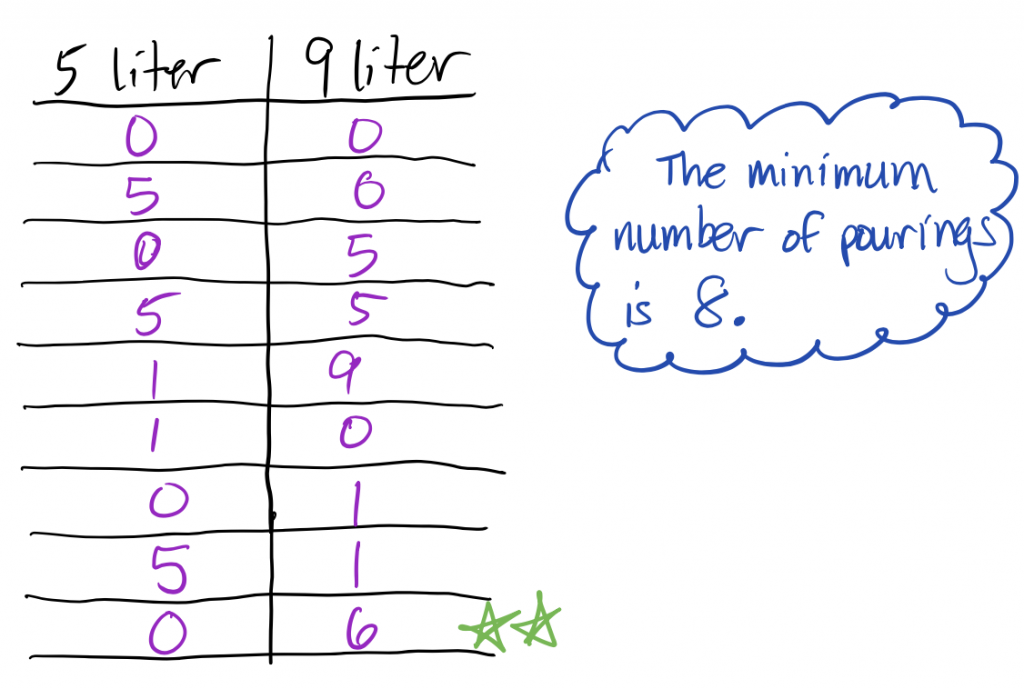
PROBLEM 2

The trick on this problem is to find a nice way to keep track of your thinking. A table like this one might work for you…
PROBLEM 3
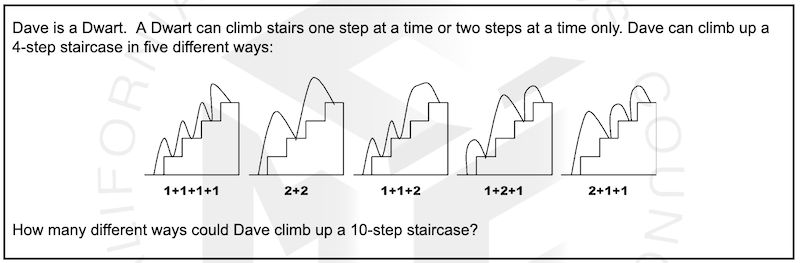
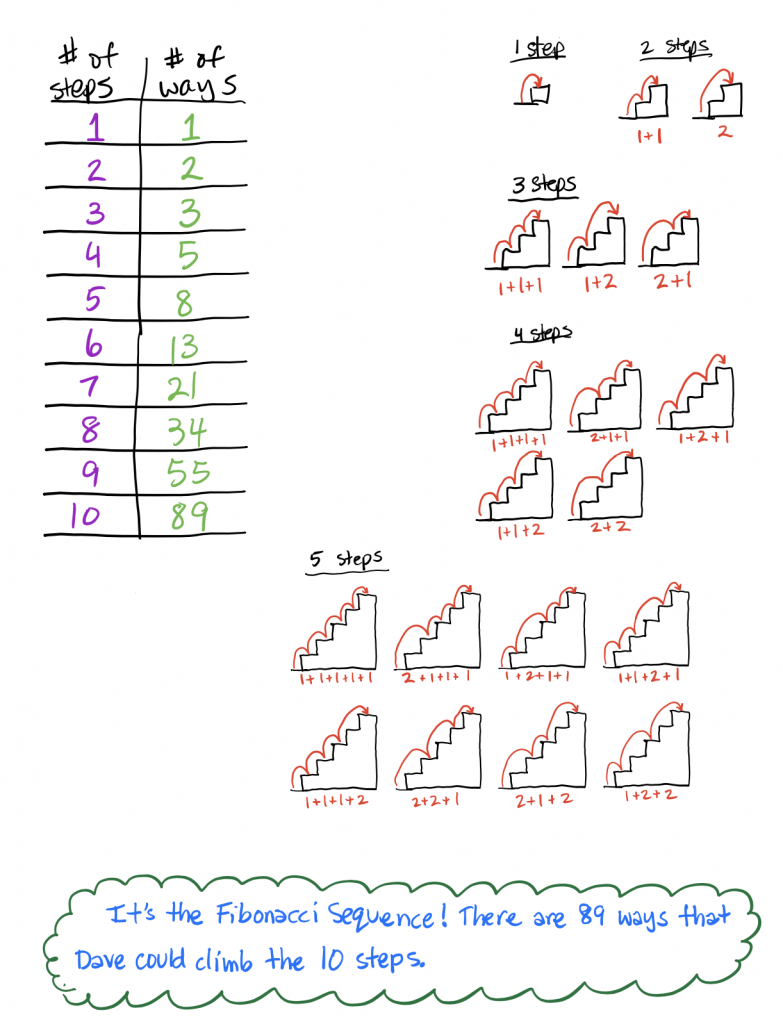
A powerful strategy for solving this problem is to NOT try to solve the 10-step staircase. Instead, find the answer for a 1-step staircase. Then find the answer for a 2-step staircase. Keep track of your answers in a table and look for a pattern.
It is likely you will see the pattern that gives you the answer for 10-steps.
Here’s what our work looks like…
PROBLEM 4

This is a lovely, but infuriating problem! Even though there are 92 correct arrangements, it is surprisingly difficult to find even ONE of the solutions.
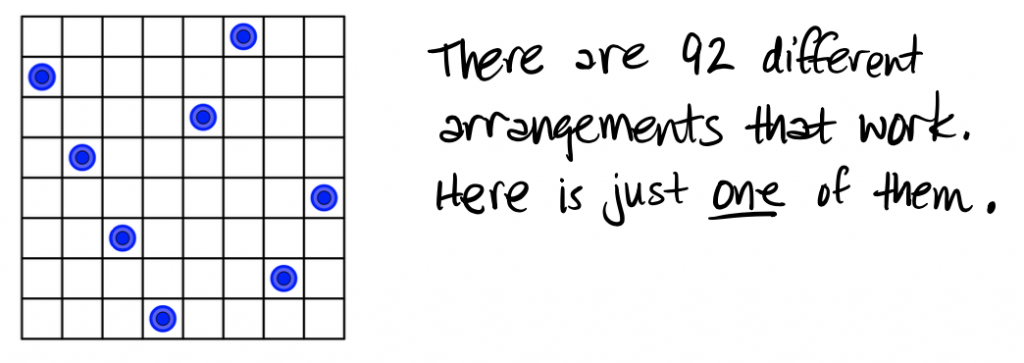
Here is a wonderful article about this problem:
https://www.quantamagazine.org/mathematician-answers-chess-problem-about-attacking-queens-20210921/
Try this cool tool…
